累乗と指数
まずは累乗について基本的なことがらを確認しましょう。数 \(a\) を6つ掛けたものは、\(aaaaaa\) と表されます。しかし、この表し方では \(a\) がいくつあるのか一見してわかりません。そこで、これを \(a^{6}\) と表します。そうすると、\(a\) が6つ掛け合わされているということがひと目見てわかります。
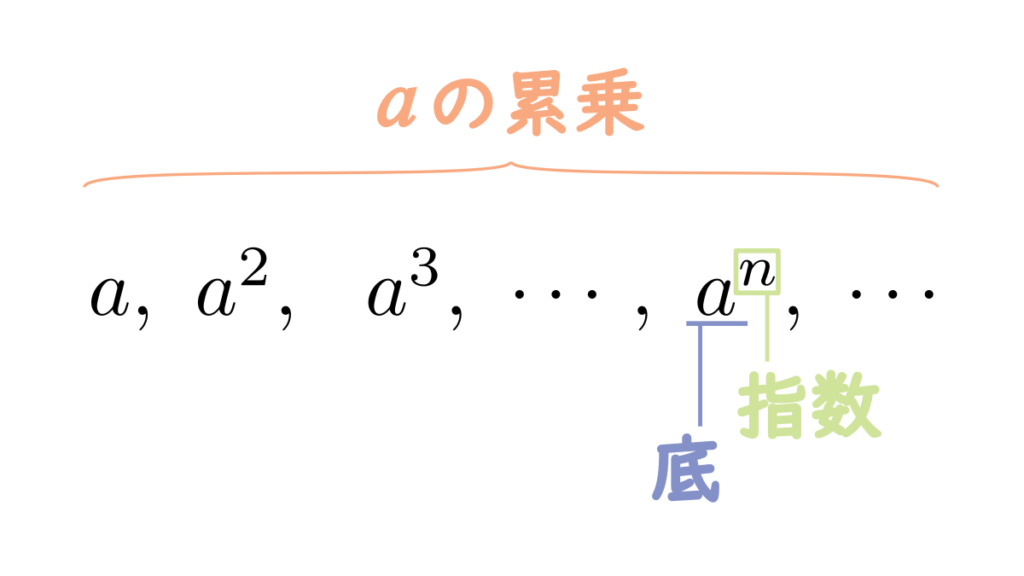
一般に、数 \(a\) を \(n\) 個掛けたものを \(a^{n}\) と表し、\(a\) の \(n\) 乗と読みます。\(2\) 乗、\(3\) 乗はそれぞれ平方、立方ともいいます。そして、\(a, a^{2}, a^{3}, \cdots\) を \(a\) の累乗といいます。また、\(a^{n}\) に対して、\(a\) を底、\(n\) を指数といいます。
指数法則
以下の指数法則は、しっかりと頭に入れて、いつでも使えるようにしましょう。
実数 \(a,b\) 、自然数 \(m,n\) に対して、以下の式が成り立つ。
\[(\mathrm{i}) \ a^{m}a^{n}=a^{m+n}\]
\[(\mathrm{ii}) \ (a^{m})^{n}=a^{mn}\]
\[(\mathrm{iii}) \ (ab)^{n}=a^{n}b^{n}\]
指数法則の証明は省略します。代わりに、以下の例題で指数法則が成り立つことを確認しましょう。
例題
以下の式を簡単な累乗の形になおしてください。
\[(1) \quad a^{3}a^{2}\]
\[(2) \quad (a^{2})^{3}\]
\[(3) \quad (ab)^{3}\]
解答・解説
掛け算の形になおしてから計算する方法
\((1)\)
\(a^{3} = aaa, \ a^{2} = aa\) なので、これを掛け合わせると \(aaaaa\) 、すなわち \(a^{5}\) になります。
\[a^{3}a^{2} = aaa \times aa = a^{5}\]
\((2)\)
\(a^{2} = aa\) が3つ掛け合わさっているので、以下のようになります。
\[(a^{2})^{3} = aa \times aa \times aa = a^{6}\]
\((3)\)
\(ab\) が3つ掛け合わさっているので、\(a, \ b\) はそれぞれ3つずつ掛け合わさっていることになります。
\[(ab)^{3} = ab \times ab \times ab = aaa \times bbb = a^{3}b^{3}\]
指数法則を使って計算する方法
\((1)\)
指数法則の \((\mathrm{i}) \ a^{m}a^{n}=a^{m+n}\) を使うと、
\[a^{3}a^{2} = a^{3+2} = a^{5}\]
となります。
\((2)\)
指数法則の \((\mathrm{ii}) \ (a^{m})^{n}=a^{mn}\) を使うと、
\[(a^{2})^{3} = a^{2 \times 3} = a^{6}\]
となります。
\((3)\)
指数法則の \((\mathrm{iii}) \ (ab)^{n}=a^{n}b^{n}\) を使うと、
\[(ab)^{3} = a^{3}b^{3}\]
となります。
このように、指数法則を使っても同じ答えとなりました。

累乗と指数法則の拡張
上で紹介した指数法則は、指数が自然数の場合に限っていました。ここからは、指数がすべての整数の場合に指数法則が成り立つように、累乗の定義を拡張します。
まずは、指数が \(0\) の場合に拡張します。\(a^{m}a^{n}=a^{m+n}\) が \(n=0\) のときに成り立つとすると
\[a^{m}a^{0}=a^{m+0}=a^{m}\]
となります。これが成り立つためには、\(a^{0}=1\) でなければなりません。よって、\(a^{0}=1\) と定義します。
次に、指数が負の整数の場合に拡張します。\(p\) を自然数として、\(a^{m}a^{n}=a^{m+n}\) が \(m=p, \ n=-p\) のときに成り立つとすると
\[a^{p}a^{-p}=a^{p-p}=a^{0}=1\]
となります。これが成り立つためには、\(\displaystyle a^{-p}=\frac{1}{a^{p}}\) でなければなりません。よって、\(\displaystyle a^{-p}=\frac{1}{a^{p}}\) と定義します。
\(a\) を実数、\(p\) を自然数とする。
\[a^{0}=1\]
\[a^{-p}=\frac{1}{a^{p}}\]
この定義は必ず頭に入れておきましょう。また、この定義に従って、0以下の整数 \(m,n\) に対して指数法則が成り立つことを確認してみてください。
練習問題
問題
以下の式を簡単な累乗の形になおしてください。なお、指数に \(0\) や負の数を用いないで表してください。ただし、\(a,b\) は実数とします。
\[(1) \quad a^{-5}a^{2}\]
\[(2) \quad a^{9}a^{-9}\]
\[(3) \quad a^{5} \div a^{2}\]
\[(4) \quad (a^{4})^{-1}\]
\[(5) \quad (ab)^{-3}\]
解答・解説
指数法則を用いて計算します。
\((1)\)
指数法則の \((\mathrm{i}) \ a^{m}a^{n}=a^{m+n}\) を使います。これは \(m\) が負の整数の場合ですが、同じように指数法則が成り立ちます。計算すると、
\[a^{-5}a^{2} = a^{-5+2} = a^{-3} = \frac{1}{a^{3}}\]
となります。
\((2)\)
\((1)\) と同じく、指数法則の \((\mathrm{i}) \ a^{m}a^{n}=a^{m+n}\) を使います。\(a^{0}=1\) であることに注意して計算すると、
\[a^{9}a^{-9} = a^{9-9} = a^{0} = 1\]
となります。
\((3)\)
割り算を分数になおすと、\(a^{2}\) が分母になります。累乗が分母にあるときは、指数の符号を反転させて掛け算の形にすることができます。実際に計算してみると、
\[a^{5} \div a^{2} = \frac{a^{5}}{a^{2}} = a^{5}a^{-2} = a^{3}\]
となります。
ここでは無理やり指数法則を使いましたが、通常は分数の形から直接約分して大丈夫です。すなわち、
\[a^{5} \div a^{2} = \frac{a^{5}}{a^{2}} = a^{3}\]
のように計算することもできます。
あるいは、「累乗の割り算は指数の引き算になる」と覚えてしまっても大丈夫です。つまり、
\[a^{5} \div a^{2} = a^{5-2} = a^{3}\]
と計算できます。
\((4)\)
指数法則の \((\mathrm{ii}) \ (a^{m})^{n}=a^{mn}\) を使います。\(a^{-4}=\frac{1}{a^{4}}\) であることに注意して計算すると、
\[(a^{4})^{-1} = a^{4 \times (-1)} = a^{-4} = \frac{1}{a^{4}}\]
となります。
\((5)\)
指数法則の \((\mathrm{iii}) \ (ab)^{n}=a^{n}b^{n}\) を使って計算すると、
\[(ab)^{-3} = a^{-3}b^{-3} = \frac{1}{a^{3}}\frac{1}{b^{3}} = \frac{1}{a^{3}b^{3}}\]
となります。
今回はこれで終わりです。この記事が気に入っていただけたら、SNS等でのシェアをよろしくお願いします!また、公式Xのフォローやブックマークなどもよろしくお願いします!

