分母の有理化【数学基礎】

分母の有理化とは

そもそも、分母の有理化とはなんでしょうか？次の式を見てください。

\[\frac{3}{\sqrt{5}+\sqrt{2}}\]

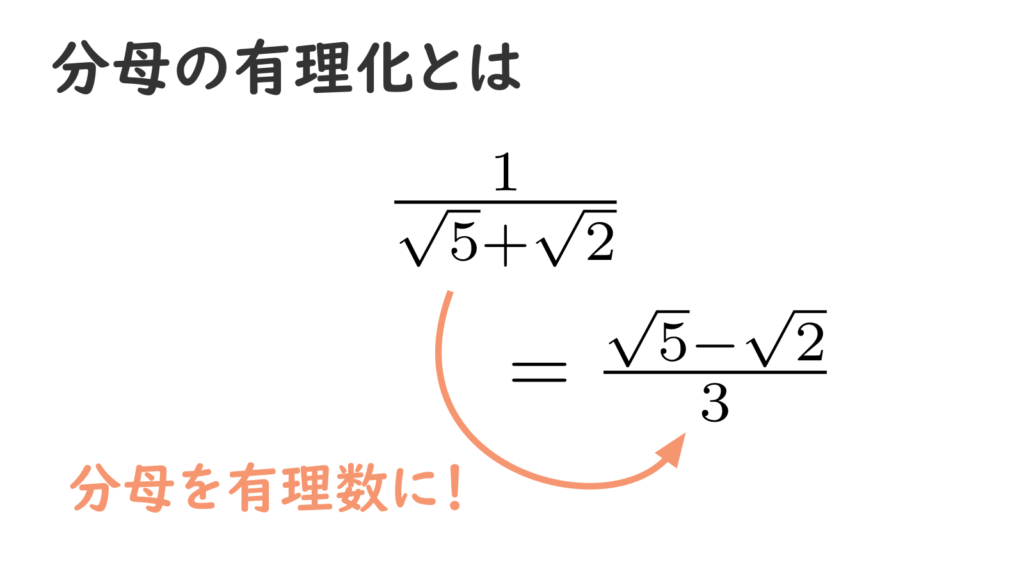
この式は、分母に無理数である \(\sqrt{5}\) や \(\sqrt{2}\) が含まれています。このように分母に無理数（特に根号）が含まれる式を、分母に無理数が含まれない形になおすことを分母の有理化といいます。

例えば、上の式で分母の有理化を行うと、

\[\frac{3}{\sqrt{5}+\sqrt{2}} = \sqrt{5}-\sqrt{2}\]

となります。具体的なやり方はこのあと解説します。

では、分母の有理化を行うと、どんなメリットがあるのでしょうか。それは、計算がしやすくなることです。例えば、分母が無理数だと、割り算によって値を求めることが難しくなります。実際に筆算をやってみるとわかりますが、分母に無限小数があると、計算が面倒になります。それ以外にも計算上のメリットがたくさんあるので、分母の有理化が重要なのです。

分母の有理化の方法

それでは、実際に分母の有理化を行う方法を確認しましょう。分母の有理化を行うときに必要な知識は主に2つです。それは、

• 分母と分子に同じ数をかけても値は変わらない
• 展開公式 \((a+b)(a-b) = a^{2}-b^{2}\)

です。どちらもよくご存知の方が多いでしょう。基本的には、この2つを利用して分母の有理化を行います。例題を通して、具体的なやり方を確認しましょう。

例題

以下の式の分母を有理化してください。

\(\displaystyle (1) \quad \frac{3}{\sqrt{12}}\)

\(\displaystyle (2) \quad \frac{1}{\sqrt{3}+\sqrt{2}}\)

\(\displaystyle (3) \quad \frac{\sqrt{5}}{1-\sqrt{2}}\)

解答・解説

\((1)\)

まずは計算をやりやすくするために、根号の中の数をなるべく小さくしましょう。

\[\frac{3}{\sqrt{12}} = \frac{3}{2\sqrt{3}}\]

それでは分母の有理化を行います。分母と分子に同じ数をかけても値は変わらないことを利用して、分母と分子に同じ数 \(\sqrt{3}\) を掛けましょう。すると

\begin{eqnarray}
\frac{3}{2\sqrt{3}} &=& \frac{3 \times \sqrt{3}}{2\sqrt{3} \times \sqrt{3}} \\[0.5em]
&=& \frac{3\sqrt{3}}{2 \times \left(\sqrt{3}\right)^{2}} \\[0.5em]
&=& \frac{3\sqrt{3}}{2 \times 3} \\[0.5em]
&=& \frac{\sqrt{3}}{2}
\end{eqnarray}

となり、有理化することができました。

\((2)\)

展開公式 \((a+b)(a-b) = a^{2}-b^{2}\) を利用すると、分母の根号をうまく取り除くことができます。ここでは、分母と分子に \(\sqrt{3}-\sqrt{2}\) を掛けましょう。すると

\begin{eqnarray}
\frac{1}{\sqrt{3}+\sqrt{2}} &=& \frac{1 \times \left(\sqrt{3}-\sqrt{2}\right)}{\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{3}-\sqrt{2}\right)} \\[0.5em]
&=& \frac{\sqrt{3}-\sqrt{2}}{\left(\sqrt{3}\right)^{2} – \left(\sqrt{2}\right)^{2}} \\[0.5em]
&=& \frac{\sqrt{3}-\sqrt{2}}{3 – 2} \\[0.5em]
&=& \sqrt{3}-\sqrt{2}
\end{eqnarray}

となります。結果的に分数の形でなくなり、すっきりした形になりました。

\((3)\)

分母に有理数と無理数が混じっていたり、分子に無理数があったりしますが、気にする必要はありません。\((2)\) と同様に、展開公式 \((a+b)(a-b) = a^{2}-b^{2}\) を利用します。分母と分子に \(1+\sqrt{2}\) を掛けると、

\begin{eqnarray}
\frac{\sqrt{5}}{1-\sqrt{2}} &=& \frac{\sqrt{5} \times \left(1+\sqrt{2}\right)}{\left(1-\sqrt{2}\right)\left(1+\sqrt{2}\right)} \\[0.5em]
&=& \frac{\sqrt{5}+\sqrt{10}}{1^{2} – \left(\sqrt{2}\right)^{2}} \\[0.5em]
&=& \frac{\sqrt{5}+\sqrt{10}}{1 – 2} \\[0.5em]
&=& \frac{\sqrt{5}+\sqrt{10}}{-1} \\[0.5em]
&=&  -\sqrt{5} -\sqrt{10}
\end{eqnarray}

となります。

---

分母の有理化の主な3パターンをまとめておきます。

以下の練習問題には、分母の有理化を用いて計算を簡単にする問題があります。ぜひチャレンジしてみてください。

練習問題

問題

以下の計算をしてください。分母は有理化してください。

\(\displaystyle (1) \quad -\frac{1}{1 + \sqrt{3}}\)

\(\displaystyle (2) \quad \frac{\sqrt{2}}{\sqrt{5} + \sqrt{2}} – \frac{1}{2 – \sqrt{7}}\)

\(\displaystyle (3) \quad \frac{1}{\sqrt{3} + \sqrt{2} – 1}\)

解答・解説

\((1)\)

分母と分子に \(1 – \sqrt{3}\) を掛けます。

\begin{eqnarray}
-\frac{1}{1 + \sqrt{3}} &=& -\frac{1 \times \left(1 – \sqrt{3}\right)}{\left(1 + \sqrt{3}\right) \times \left(1 – \sqrt{3}\right)} \\[0.5em]
&=& -\frac{1 – \sqrt{3}}{1^{2} – \left(\sqrt{3}\right)^{2}} \\[0.5em]
&=& -\frac{1 – \sqrt{3}}{1 – 3} \\[0.5em]
&=& -\frac{1 – \sqrt{3}}{-2} \\[0.5em]
&=& \frac{1 – \sqrt{3}}{2}
\end{eqnarray}

\((2)\)

先に分母の有理化を行うことによって、計算が簡単になる例です。まずは、2つの分数それぞれの分母を有理化します。

\begin{eqnarray}
\frac{\sqrt{2}}{\sqrt{5} + \sqrt{2}} – \frac{1}{2 – \sqrt{7}} &=& \frac{\sqrt{2} \times \left(\sqrt{5} – \sqrt{2}\right)}{\left(\sqrt{5} + \sqrt{2}\right) \times \left(\sqrt{5} – \sqrt{2}\right)} – \frac{1 \times \left(2 + \sqrt{7}\right)}{\left(2 – \sqrt{7}\right) \times \left(2 + \sqrt{7}\right)} \\[0.5em]
&=& \frac{\sqrt{10} – 2}{5 – 2} – \frac{2 + \sqrt{7}}{4 – 7} \\[0.5em]
&=& \frac{\sqrt{10} – 2}{3} – \frac{2 + \sqrt{7}}{-3} \\[0.5em]
&=& \frac{\sqrt{10} – 2}{3} + \frac{2 + \sqrt{7}}{3}
\end{eqnarray}

そうすると分母が揃うので、そのまま計算を進めましょう。

\begin{eqnarray}
\frac{\sqrt{10} – 2}{3} + \frac{2 + \sqrt{7}}{3} &=& \frac{\sqrt{10} – 2 + 2 + \sqrt{7}}{3} \\[0.5em]
&=& \frac{\sqrt{10} + \sqrt{7}}{3}
\end{eqnarray}

今回の例では、偶然にも分母が一致してそのまま計算することができました。しかし、仮に分母が一致しなくても、分母が有理化されていると通分がしやすくなるので、分母の有理化を行うメリットは大いにあります。

\((3)\)

分母の項が3つになっても恐れる必要はありません。分母を \(\left(\sqrt{3} + \sqrt{2}\right) – 1\) のように、\(\sqrt{3} + \sqrt{2}\) をひとまとまりとして考えます。すると、分母と分子に \(\left(\sqrt{3} + \sqrt{2}\right) + 1\) を掛けるという発想が浮かんでくるでしょう。なお、以下の計算では、展開公式 \((a+b)^{2} = a^{2} + 2ab + b^{2}\) を使っています。

\begin{eqnarray}
\frac{1}{\sqrt{3} + \sqrt{2} – 1} &=& \frac{1 \times \left\{\left(\sqrt{3} + \sqrt{2}\right) + 1\right\}}{\left\{\left(\sqrt{3} + \sqrt{2}\right) – 1\right\} \times \left\{\left(\sqrt{3} + \sqrt{2}\right) + 1\right\}} \\[0.5em]
&=& \frac{\sqrt{3} + \sqrt{2} + 1}{\left(\sqrt{3} + \sqrt{2}\right)^{2} – 1^{2}} \\[0.5em]
&=& \frac{\sqrt{3} + \sqrt{2} + 1}{\left(\sqrt{3}\right)^{2} + 2\sqrt{3}\sqrt{2} + \left(\sqrt{2}\right)^{2} – 1^{2}} \\[0.5em]
&=& \frac{\sqrt{3} + \sqrt{2} + 1}{3 + 2\sqrt{6} + 2 – 1} \\[0.5em]
&=& \frac{\sqrt{3} + \sqrt{2} + 1}{4 + 2\sqrt{6}} \\[0.5em]
&=& \frac{\sqrt{3} + \sqrt{2} + 1}{2\left(2 + \sqrt{6}\right)}
\end{eqnarray}

上の計算がわかりにくい人は、\(\sqrt{3} + \sqrt{2}\) を適当な文字でおいて展開しましょう。置き換えを利用した展開については以下の記事をご覧ください。

ここまで来たら、あとは今までと同じように分母の有理化をするだけです。ここでは、分母の \(2\) をくくりだしていますが、このような場合はこの \(2\) を一旦無視して分母の有理化をすることができます。すなわち、分母と分子に \(2 – \sqrt{6}\) を掛けます。

\begin{eqnarray}
\frac{\sqrt{3} + \sqrt{2} + 1}{2\left(2 + \sqrt{6}\right)} &=& \frac{\left(\sqrt{3} + \sqrt{2} + 1\right) \times \left(2 – \sqrt{6}\right)}{2\left(2 + \sqrt{6}\right) \times \left(2 – \sqrt{6}\right)} \\[0.5em]
&=& \frac{2\sqrt{3} – \sqrt{18} + 2\sqrt{2} – \sqrt{12} + 2 – \sqrt{6}}{2 \left\{2^{2} – \left(\sqrt{6}\right)^{2}\right\}} \\[0.5em]
&=& \frac{2\sqrt{3} – 3\sqrt{2} + 2\sqrt{2} – 2\sqrt{3} + 2 – \sqrt{6}}{2 \left(4 – 6\right)} \\[0.5em]
&=& \frac{-\sqrt{2} + 2 – \sqrt{6}}{2 \times (-2)} \\[0.5em]
&=& \frac{-\sqrt{2} + 2 – \sqrt{6}}{-4} \\[0.5em]
&=& \frac{\sqrt{2} + \sqrt{6} -2}{4}
\end{eqnarray}

このように、順を追って考えれば、分母が3項以上であっても有理化することができます。

---

今回はこれで終わりです。この記事が気に入っていただけたら、SNS等でのシェアをよろしくお願いします！また、公式Xのフォローやブックマークなどもよろしくお願いします！

質問・感想等はぜひ下のコメント欄に書き込んでください！