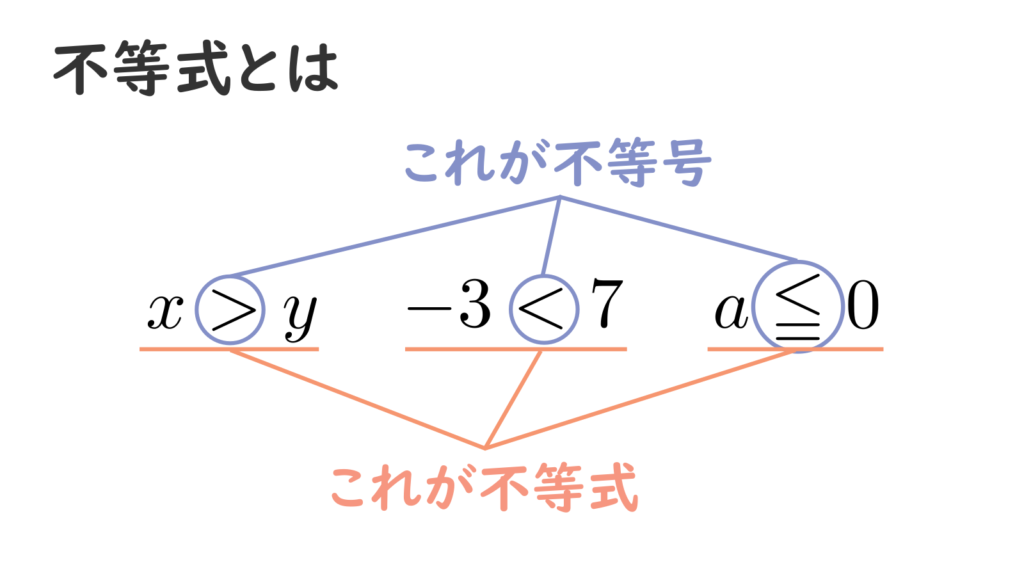
不等式とは
実数や式の大小関係を表す式を不等式といいます。\(a, \ b\) を実数としたとき、
- \(a\) が \(b\) より大きいことを \(a > b\)
- \(a\) が \(b\) より小さいことを \(a < b\)
- \(a\) が \(b\) より大きいか、または等しいことを \(a ≧ b\)
- \(a\) が \(b\) より小さいか、または等しいことを \(a ≦ b\)
などと表します。このとき、記号 \(>, \ <, \ ≧, \ ≦\) を不等号といい、それぞれ大なり、小なり、大なりイコール、小なりイコールなどと読みます。
また、上に述べたことの言い換えにすぎませんが、
- \(a\) が \(b\) 以上であることを \(a ≧ b\)
- \(a\) が \(b\) 以下であることを \(a ≦ b\)
- \(a\) が \(b\) 未満であることを \(a < b\)
と表します。
なお、\(a ≧ b\) は「\(a > b\) または \(a = b\)」が成り立つことを意味します。つまり、\(2 ≧ 1\) や \(1 ≧ 1\) はどちらも正しい不等式です。\(≦\) についても同様です。
余談ですが、不等式は実数の世界でのみ考えます。実数と複素数の間や、複素数どうしの間では、大小関係を考えることはできません。その理由についての説明は、のちの記事に託すことにします。
不等式の基本性質
不等式の基本性質として、以下の性質をみとめることにします。重要な性質なのでぜひ覚えましょう。
- 2つの実数 \(a, \ b\) に対して
\[a < b, \ a = b, \ a > b\]
のうち、どれか1つだけが成り立つ。
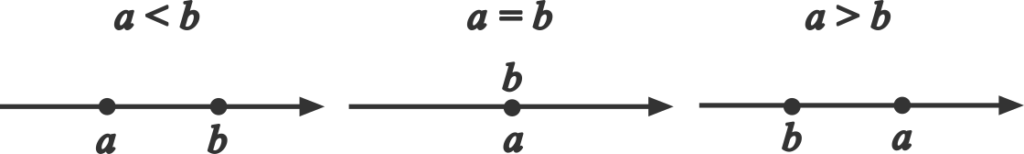
- \(a > b, \ b > c\) ならば \(a > c\)
- \(a > b\) ならば \(a+c > b+c\)
- \(a>b, \ c>0\) ならば \(ac > bc\)
\(a>b, \ c<0\) ならば \(ac < bc\)
特に性質4には注意が必要です。不等式の両辺に同じ正の実数を掛けても不等号の向きは変わりませんが、両辺に同じ負の実数を掛けると不等号の向きが逆になります。
これらの基本性質を使った例題を1つ解いてみましょう。
例題
\(x > 3\) のとき、以下の式のとりうる値の範囲を考えてください。
\((1) \quad x+2\)
\((2) \quad x-5\)
\((3) \quad 3x\)
\((4) \quad -2x\)
解答・解説
\((1)\)
性質3より、不等式の両辺に同じ実数を足しても大小関係は変わらないので、\(x > 3\) の両辺に \(2\) を足すと、
\[x+2 > 3+2\]
となります。よって、
\[x+2 > 5\]
\((2)\)
同じく性質3より、\(x > 3\) の両辺に \(-5\) を足すと、
\[x-5 > 3-5\]
となります。よって、
\[x-5 > -2\]
このことから、不等式の両辺から同じ実数を引いても大小関係は変わらないことがわかります。
\((3)\)
性質4より、不等式の両辺に同じ正の実数を掛けても大小関係は変わらないので、\(x > 3\) の両辺に \(3\) を掛けると、
\[x \times 3 > 3 \times 3\]
となります。よって、
\[3x > 9\]
\((4)\)
性質4より、不等式の両辺に同じ負の実数を掛けると大小関係が逆になるので、\(x > 3\) の両辺に \(-2\) を掛けると、
\[x \times (-2) < 3 \times (-2)\]
となります。不等号の向きが逆になっていることに注意してください。
よって、
\[-2x < -6\]
不等式の諸性質
ここからは、先ほど紹介した基本性質から、不等式に関するさまざまな諸性質を導いていきます。どれも不等式を解く際に必要な知識ですが、経験を積むうちに身につけられるので、無理に暗記する必要はありません。それよりも、公理から定理を導くという数学の真髄を体験してください。
なお、\(A \Longrightarrow B\) は「AならばBが成り立つ」ことを、\(A \Longleftrightarrow B\) は「AならばBが成り立ち、かつBならばAが成り立つ」ことを意味します。
- \(a>b+c \Longleftrightarrow a-b>c\)
証明
性質3より、\(a>b+c\) の両辺に \(-b\) を足すと、
\[a-b>b-b+c\]
\[a-b>c\]
これで \(a>b+c \Longrightarrow a-b>c\) が証明できました。
逆に、\(a-b>c\) の両辺に \(b\) を足すと、
\[a-b+b>c+b\]
\[a>b+c\]
これで \(a>b+c \Longleftarrow a-b>c\) が証明できました。
以上より \(a>b+c \Longleftrightarrow a-b>c\) が成り立ちます。■
この例のように、\(A \Longleftrightarrow B\) を証明する際は、\(A \Longrightarrow B\) と \(A \Longleftarrow B\) をともに証明する必要があります。
なお性質5より、不等式においても等式と同様に移項を行うことができます。
- \(a>b \iff a-b>0\)
証明
性質5で、\(c=0\) とおくと
\[a>b+0 \Longleftrightarrow a-b>0\]
\[a>b \Longleftrightarrow a-b>0\]
となります。■
- \(a<0 \Longleftrightarrow -a>0\)
証明
性質3より、\(a<0\) の両辺に \(-a\) を足すと、
\[a-a<0-a\]
\[0<-a\]
\[-a>0\]
逆に、\(-a>0\) の両辺に \(a\) を足すと、
\[-a+a>0+a\]
\[0>a\]
\[a<0\]
以上より \(a<0 \Longleftrightarrow -a>0\) が成り立ちます。■
- \(-a>-b \Longleftrightarrow a<b\)
証明
性質6より、
\[-a>-b\]
\[-a-(-b)>0\]
\[-a+b>0\]
再び性質6を用いて、
\[b>a\]
\[a<b\]
となり、\(-a>-b \Longrightarrow a<b\) が成り立つことがわかります。
逆に \(-a>-b \Longleftarrow a<b\) が成り立つことは、上の計算を逆にたどれば示すことができます。■
なお、性質7と性質8は、性質4から導くこともできます。
- \(a>0, \ b>0 \Longrightarrow a+b>0\)
証明
性質3より、\(a>0\) の両辺に \(b\) を足すと、
\[a+b>0+b\]
\[a+b>b\]
これと \(b>0\) から、性質2より \(a+b>0\) となります。■
- \(a>0, \ b>0 \Longrightarrow ab>0\)
- \(a>0, \ b<0 \Longrightarrow ab<0\)
- \(a<0, \ b>0 \Longrightarrow ab<0\)
- \(a<0, \ b<0 \Longrightarrow ab>0\)
証明
性質10を証明します。
性質4より、\(a>0\) の両辺に \(b\) を掛けると、
\[a \times b>0 \times b\]
\[ab>0\]
となります。性質11、12、13も同様に証明できます。■
これらの性質は、同符号どうしの積は正、異符号どうしの積は負であることを示しています。
- \(\displaystyle a>0 \Longrightarrow \frac{1}{a}>0\)
- \(\displaystyle a<0 \Longrightarrow \frac{1}{a}<0\)
証明
性質14を証明します。
\(a>0\) のとき、\(\displaystyle \frac{1}{a}<0\) と仮定します。
すると、性質11より
\[a \cdot \frac{1}{a} < 0\]
\[1<0\]
となり、\(1>0\) であることに矛盾します。よって、\(\displaystyle \frac{1}{a}>0\) です。
性質15も同様に証明できます。■
この証明には背理法を利用しました。
- \(\displaystyle a>0, \ b>0 \Longrightarrow \frac{a}{b}>0\)
- \(\displaystyle a>0, \ b<0 \Longrightarrow \frac{a}{b}<0\)
- \(\displaystyle a<0, \ b>0 \Longrightarrow \frac{a}{b}<0\)
- \(\displaystyle a<0, \ b<0 \Longrightarrow \frac{a}{b}>0\)
証明
性質16を証明します。
\(b>0\) から、性質14より \(\displaystyle \frac{1}{b}>0\) です。
\(\displaystyle a>0, \ \frac{1}{b}>0\) から、性質10より、
\[a \cdot \frac{1}{b} > 0\]
\[\frac{a}{b} > 0\]
となります。性質17、18、19も同様に証明できます。■
これらの性質は、同符号どうしの商は正、異符号どうしの商は負であることを示しています。
- \(\displaystyle a>b, c>0 \Longrightarrow \frac{a}{c}>\frac{b}{c}\)
- \(\displaystyle a>b, c<0 \Longrightarrow \frac{a}{c}<\frac{b}{c}\)
証明
性質20を証明します。
\(c>0\) から、性質14より \(\displaystyle \frac{1}{c}>0\) です。
\(\displaystyle a>b, \ \frac{1}{c}>0\) から、性質4より、
\[a \cdot \frac{1}{c} > b \cdot \frac{1}{c}\]
\[\frac{a}{c}>\frac{b}{c}\]
となります。性質21も同様に証明できます。■
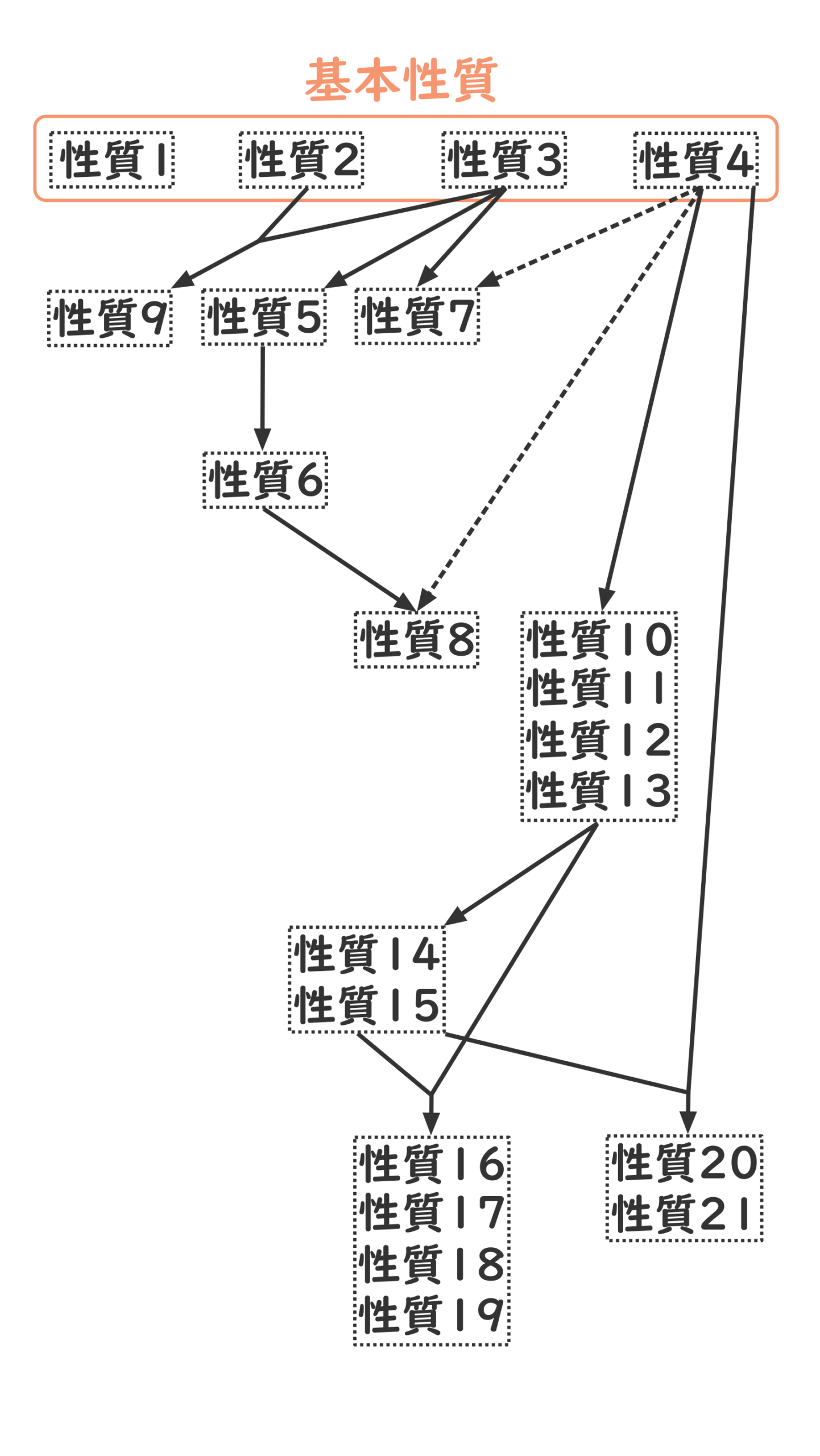
最後に、諸性質の「系統図」のようなものを描いてみました。図中の矢印は、始点の性質から終点の性質が導かれることを示しています。少ない公理から多くの定理を芋づる式に導くことは、数学の醍醐味の一つです!
練習問題
問題
\(a>0, \ b>0, \ c<0, \ d<0\) のとき、以下の式のとりうる値の範囲を考えてください。
\((1) \quad ab+cd\)
\((2) \quad (a-d)(b-c)\)
\(\displaystyle (3) \quad \frac{ac}{bd}\)
解答・解説
\((1)\)
\(a>0 ,\ b>0\) から、性質10より
\[ab>0\]
また、\(c<0 ,\ d<0\) から、性質13より
\[cd>0\]
よって、\(ab>0 ,\ cd>0\) から、性質9より
\[ab+cd>0\]
\((2)\)
\(c<0, \ d<0\) から、性質7より
\[-c>0, \ -d>0\]
\(a>0, \ -d>0\) と \(b>0, \ -c>0\) から、性質9より
\[a-d>0, \ b-c>0\]
よって、性質10より
\[(a-d)(b-c)>0\]
\((3)\)
\(a>0, \ c<0\) と \(b>0, \ d<0\) から、性質11より
\[ac<0, \ bd<0\]
よって、性質19より
\[\frac{ac}{bd}>0\]
今回はこれで終わりです。この記事が気に入っていただけたら、SNS等でのシェアをよろしくお願いします!また、公式Xのフォローやブックマークなどもよろしくお願いします!
質問・感想等はぜひ下のコメント欄に書き込んでください!

