連立1次不等式の解き方
1次不等式の解き方はすでにマスターしているでしょうか?自信がない場合は以下の記事を先にお読みください。

いくつかの不等式を組み合わせたものを連立不等式といいます。また、すべての不等式を同時に成り立たせるような \(x\) の範囲を求めることを、連立不等式を解くといいます。そして、そのような範囲のことを連立不等式の解といいます。
例えば、
$$
\begin{cases}
x+3>0 \\
2x-5≦0
\end{cases}
$$
$$
\begin{cases}
2x^{2}+1≧-x \\
x^{3}>5+2x
\end{cases}
$$
$$
\begin{cases}
6<a \\
a^{2}+3a-5≦0 \\
3a>a+7
\end{cases}
$$
などが連立不等式です。連立方程式の不等式バージョンということですね。
今回は、連立不等式の中でも、連立1次不等式のみを取り扱います。つまり、すべての不等式が1次不等式の連立不等式ということです。
連立不等式を解く際に重要なのが、不等式の解を数直線上に表せることです。まずはその練習をしてみましょう。
例題1
以下の不等式を数直線上の範囲として表してください。ただし、端の点が含まれる場合は黒丸で、含まれない場合は白丸で表してください。
\((1) \quad x>2\)
\((2) \quad -3<y≦5\)
\((3) \quad
\begin{cases}
a<8 \\
a≧1
\end{cases}
\)
※2つの不等式を同時に満たす範囲を考えてください。
解答・解説
\((1)\)
\(x\) が \(2\) より大きいということは、数直線上で \(2\) よりも右側にある部分全体が \(x\) のとりうる値の範囲です。すなわち、下図のようになります。ただし、端の点は含みません。
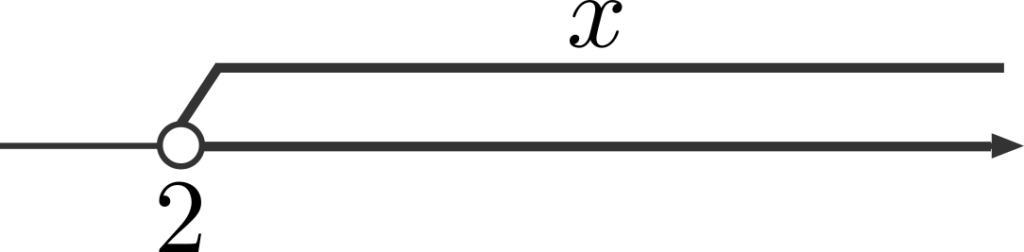
\((2)\)
\(y\) が \(-3\) より大きく、\(5\) 以下なので、数直線上の \(-3\) と \(5\) の間の部分が \(y\) のとりうる値の範囲です。ただし、\(-3\) は含まず、\(5\) は含みます。よって、下の図のようになります。
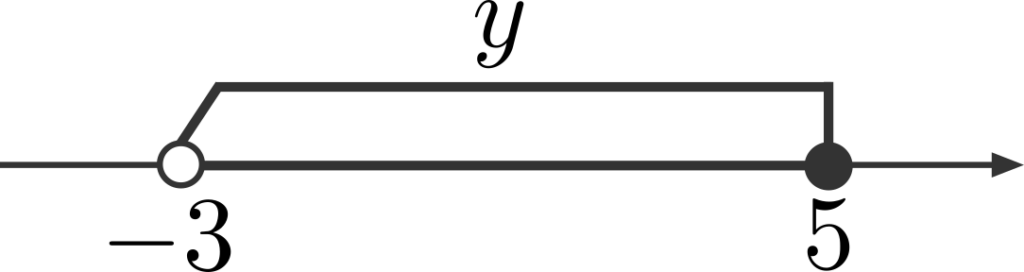
\((3)\)
2つの不等式がありますが、とりあえずどちらも数直線上に図示してみましょう。\(a<8\) は数直線上で \(8\) よりも左側の部分、\(a≧1\) は数直線上で \(1\) とその右側の部分を表します。
実際に図示すると、下図のように2つの範囲が重なる部分があることが分かります。この部分(図の斜線部)こそが2つの不等式が表す値の範囲です。
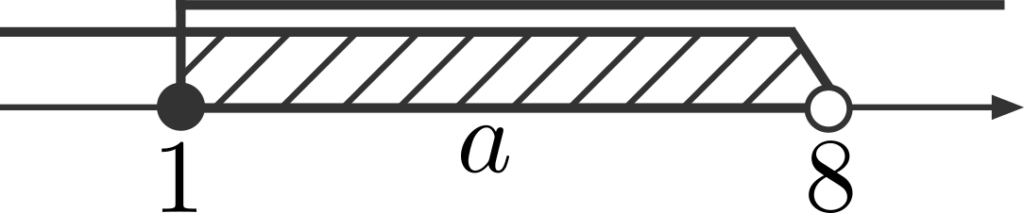
例題1の \((3)\) は、2つの不等式から1つの範囲を求めましたが、これは連立不等式を解く手順そのものです。例えば、不等式が2つの連立1次不等式を解くと2つの不等式が解として出てきますが、それらを上のようにして1つの範囲にまとめるのです。つまり、例題1が理解できれば、連立不等式は半分マスターしたといっても過言ではありません。
それでは、次の例題で実際に連立1次不等式を解いてみましょう。
例題2
以下の連立不等式を解いてください。
\((1) \quad
\begin{cases}
3x<9 \\
x+2>0
\end{cases}
\)
\((2) \quad
\begin{cases}
1-x<0 \\
5x-4≧2
\end{cases}
\)
\((3) \quad
\begin{cases}
2x+5>0 \\
3x≧7x+12
\end{cases}
\)
解答・解説
読んでいる方がすでに1次不等式を習熟されていることを前提に、不等式の詳しい解法については省略します。必要であれば、記事の最初で紹介した記事をお読みください。
\((1)\)
2つの不等式を解くと、
$$
\begin{cases}
x<3 \\
x>-2
\end{cases}
$$
となります。
これらを数直線上に図示すると、下の図のようになります。
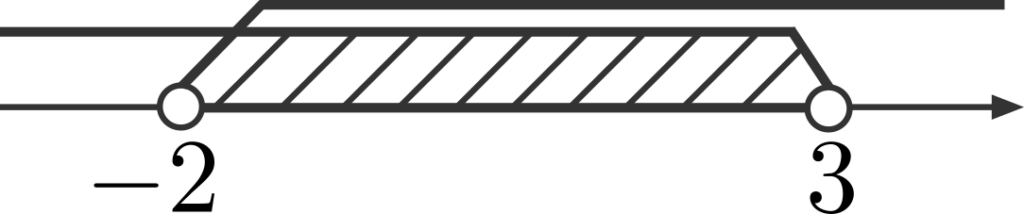
よって、斜線部の範囲を再び不等式に表すと、
\[-2<x<3\]
となります。
(答)\(-2<x<3\)
\((2)\)
2つの不等式を解くと、
$$
\begin{cases}
x>1 \\
\displaystyle x≧\frac{6}{5}
\end{cases}
$$
となります。
これらを数直線上に図示すると、下の図のようになります。
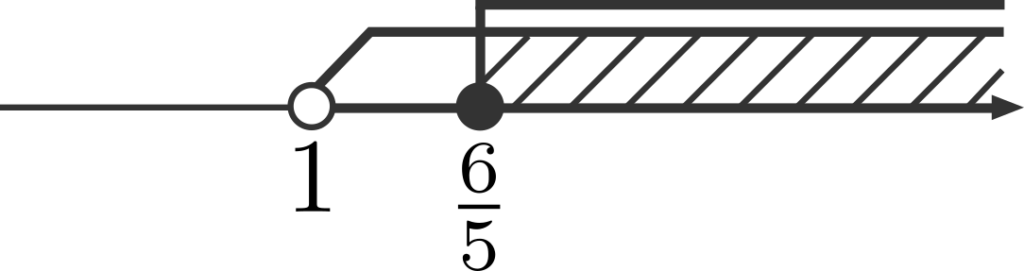
よって、斜線部の範囲を再び不等式に表すと、
\[x≧\frac{6}{5}\]
となります。
(答)\(\displaystyle x≧\frac{6}{5}\)
\((3)\)
2つの不等式を解くと、
$$
\begin{cases}
\displaystyle x>-\frac{5}{2} \\
x≦-3
\end{cases}
$$
となります。
これらを数直線上に図示すると、下の図のようになります。
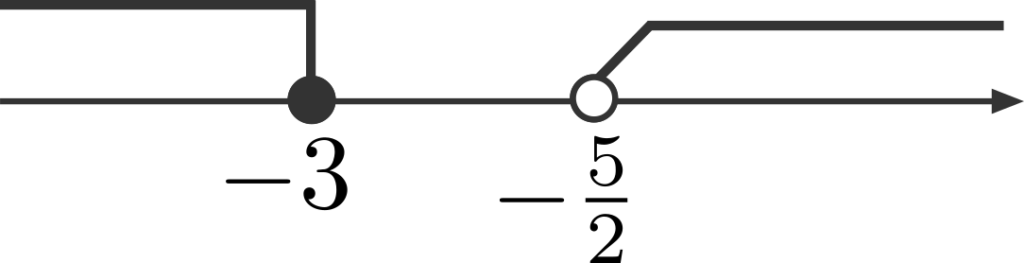
図から分かるとおり、2つの不等式に共通する範囲はありません。よって、この連立不等式は解をもちません。
(答)解はない
練習問題
問題
以下の連立不等式を解いてください。
\((1) \quad
\begin{cases}
\displaystyle \frac{x}{3}+\frac{1}{2}>\frac{1}{4} \\
x+5≧4x-1
\end{cases}
\)
\((2) \quad x+2<4x-1<3x+4\)
\((3) \quad
\begin{cases}
5x≦3 \\
2x>3x+1 \\
\sqrt{2}x+3≧1
\end{cases}
\)
解答・解説
\((1)\)
2つの不等式を解くと、
$$
\begin{cases}
\displaystyle x>-\frac{3}{4} \\
x≦2
\end{cases}
$$
となります。
これらを数直線上に図示すると、下の図のようになります。
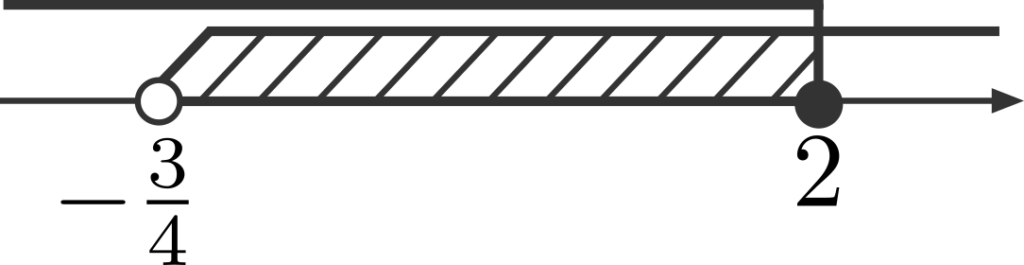
よって、斜線部の範囲を再び不等式に表すと、
\[-\frac{3}{4}<x≦2\]
となります。
(答)\(\displaystyle -\frac{3}{4}<x≦2\)
\((2)\)
2つの不等式が1つにまとめられたパターンです。このような不等式は、2つの不等式に分けて連立不等式として解きます。すなわち、
$$
\begin{cases}
x+2<4x-1 \\
4x-1<3x+4
\end{cases}
$$
という連立不等式を解けば良いということです。
2つの不等式を解くと、
$$
\begin{cases}
x>1 \\
x<5
\end{cases}
$$
となるので、これらを数直線上に図示すると下の図のようになります。(これくらい単純な不等式であれば、数直線を書かなくてもまとめられるようになりたいですね)
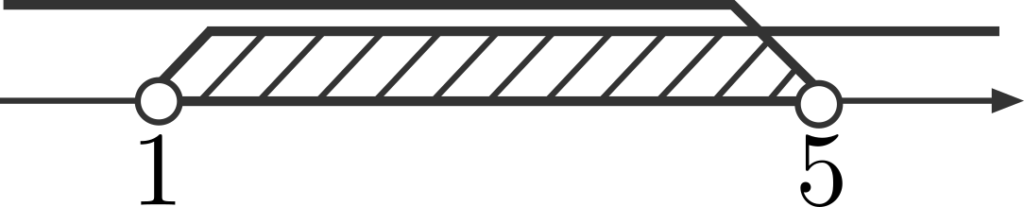
よって、斜線部の範囲を再び不等式に表すと、
\[1<x<5\]
となります。
(答)\(1<x<5\)
\((3)\)
不等式が3つに増えましたが、やることは変わりません。
3つの不等式を解くと、
$$
\begin{cases}
\displaystyle x≦\frac{3}{5} \\
x<-1 \\
x≧-\sqrt{2}
\end{cases}
$$
となるので、これらを数直線上に図示すると下の図のようになります。
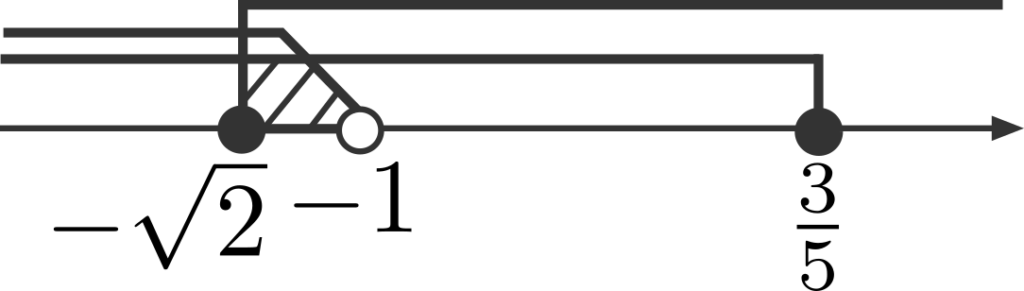
3つの不等式の共通部分は図の斜線部なので、この範囲を再び不等式に表すと、
\[-\sqrt{2}≦x<-1\]
となります。
(答)\(-\sqrt{2}≦x<-1\)
今回はこれで終わりです。この記事が気に入っていただけたら、SNS等でのシェアをよろしくお願いします!また、公式Xのフォローやブックマークなどもよろしくお願いします!
質問・感想等はぜひ下のコメント欄に書き込んでください!