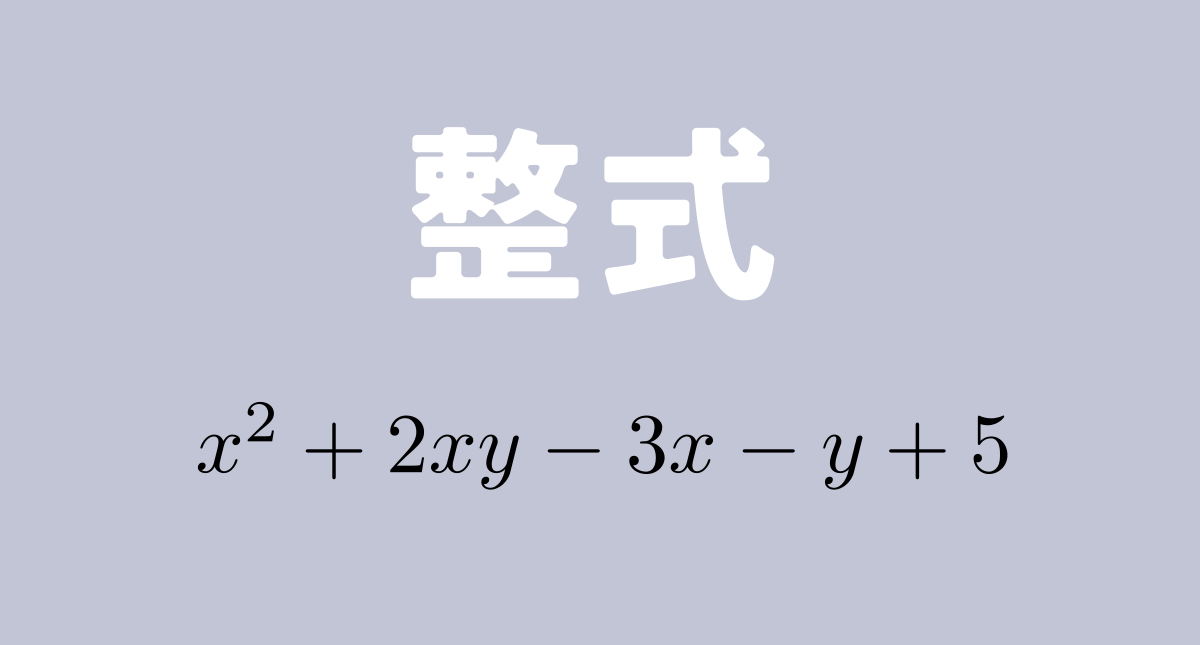単項式
数や文字を掛け合わせてできる式を単項式といいます。例えば、
\[2x, \ -3x^{2}, \ 6ab\]
などは単項式です。また、数や文字だけの式も単項式です。つまり、
\[4, \ x, \ a^{2}\]
なども単項式です。
単項式の中で、数の部分をその単項式の係数といいます。また、掛け合わされている文字の個数をその単項式の次数といいます。例えば、
- \(2x\) の係数は \(2\) 、次数は \(1\)
- \(-3a^{2}\) の係数は \(-3\) 、次数は \(2\)
- \(6xy\) の係数は \(6\) 、次数は \(2\)
- \(x\) の係数は \(1\) 、次数は \(1\)
です。\(x\) や \(y^{2}\) のような文字だけの単項式は、文字の前に \(1\) が掛けられていると考えるので、係数は \(1\) になります。
数を単項式と考えるときは、係数はその数自身、次数は \(0\) と考えます。例えば、\(4\) という単項式の係数は \(4\) 、次数は \(0\) です。
多項式
単項式の和として表される式を多項式といいます。例えば、\(3x^{2}, \ x, \ -5\) という3つの単項式を足し合わせると、
\[3x^{2}+x+(-5) = 3x^{2}+x-5\]
という多項式になります。
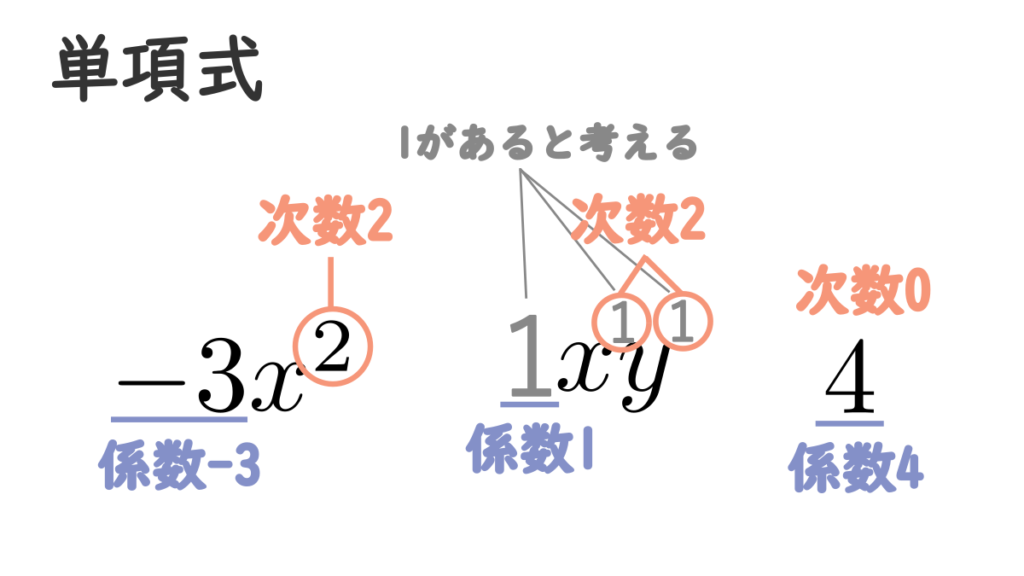
多項式に含まれる単項式を、その多項式の項といいます。例えば、\(3x^{2}+x-5\) という多項式の項は \(3x^{2}, \ x, \ -5\) です。
多項式の項のうち、文字を含まないものを定数項といいます。\(3x^{2}+x-5\) の定数項は \(-5\) です。
整式
単項式と多項式を合わせて整式といいます。ただし、単項式は項が1つの多項式と考えることができるので、整式と多項式は実質的に同じ意味です。
整式の項の係数は、整数である必要はありません。つまり、
\[-\frac{2}{3}xy + \sqrt{7}x + 0.2y – \pi\]
のような式も整式です。
一方、単項式の和として表せない式は、整式ではありません。例えば、
\[\frac{2x-3}{x^{2}+5}\]
\[3^{x}-\sin{x}\]
のような式は整式ではありません。
ある整式において、最も次数が高い項の次数を、その整式の次数といいます。また、次数が \(n\) の整式を \(n\)次式といいます。例えば、
- \(3x^{2}+x-5\) の次数は \(2\) で、この式は \(2\)次式
- \(4a-b^{3}+1\) の次数は \(3\) で、この式は \(3\)次式
- \(x^{3}y^{2}-4xy+3x+y\) の次数は \(5\) で、この式は \(5\)次式
です。
整式の次数は、着目する文字によって変わることがあります。ある文字に着目したとき、それ以外の文字は数として考えます。例えば、
\[x^{3}y^{2}-4xy+3x+y\]
という整式は、\(x\) と \(y\) に着目したときは \(5\)次式ですが、\(x\) に着目すると \(3\)次式、\(y\) に着目すると \(2\)次式になります。また、\(y\) に着目すると、\(-4xy\) という項の係数は \(-4x\) に、\(3x\) という項は定数項になります。

整式の整理
整式の中で、文字の部分が同じ項を同類項といいます。例えば、
\[xy^{2}, \ -3xy^{2}, \ \frac{xy^{2}}{5}, \ \sqrt{7}xy^{2}, \ 2y^{2}x\]
はすべて同類項です。
同類項は係数部分を足し合わせることで、1つの項にまとめることができます。例えば、
\begin{eqnarray}
5x^{2}+x^{2}-3x^{2} &=& (5+1-3)x^{2} \\[0.5em]
&=& 3x^{2}
\end{eqnarray}
のように同類項をまとめることができます。同類項をまとめることを、整式を整理するといいます。
整式の次数を判断するときは、まず同類項をまとめる必要があります。例えば、\(2x^{2}+3x-2x^{2}+1\) という式は、
\[2x^{2}+3x-2x^{2}+1 = 3x+1\]
と整理できるので、\(1\)次式です。
整式を見やすくするために、項の次数の順に並びかえることがあります。項の次数が高い順に並べることを、降べきの順に整理するといいます。一方、項の次数が低い順に並べることを、昇べきの順に整理するといいます。
例えば、\(-2x+3x^{3}+x^{2}-5\) という式を、
- 降べきの順に整理すると \(3x^{3}+x^{2}-2x-5\)
- 昇べきの順に整理すると \(-5-2x+x^{2}+3x^{3}\)
となります。
整式の整理や並びかえのときにも、特定の文字に着目して整理することができます。そのときも、着目していない文字を数として考えれば大丈夫です。
練習問題
問題
整式
\[2x^{3}y^{2}+xy^{3}+2x^{2}+x^{3}y^{2}-y+4+y^{3}-3x^{3}y^{2}+x^{2}\]
の同類項をまとめて整理し、降べきの順に整理したうえで、整式の次数と定数項を答えてください。また、文字 \(x\) に着目したときの次数と定数項を答えてください。
解答・解説
まずは同類項をまとめて整理します。式を見ると、\(x^{3}y^{2}\) の項と、\(x^{3}\) の項をまとめることができそうです。実際に整理すると、
\begin{align}
&2x^{3}y^{2}+xy^{3}+2x^{2}+x^{3}y^{2}-y+4+y^{3}-3x^{3}y^{2}+x^{2} \\[0.5em]
&= 2x^{3}y^{2}+x^{3}y^{2}-3x^{3}y^{2}+xy^{3}+2x^{2}+x^{2}-y+4+y^{3} \\[0.5em]
&= (2+1-3)x^{3}y^{2}+xy^{3}+(2+1)x^{2}-y+4+y^{3} \\[0.5em]
&= xy^{3}+3x^{2}-y+4+y^{3}
\end{align}
となります。次に、式を降べきの順に整理します。項の次数が高い順に並べると、
\[xy^{3}+3x^{2}-y+4+y^{3} = xy^{3}+y^{3}+3x^{2}-y+4\]
となります。ここで、最も次数が高い項は \(xy^{3}\) で、その次数は \(4\) です。また、定数項は \(4\) です。
続いて、\(x\) に着目して降べきの順に整理します。このとき、着目しない \(y\) は数として考えます。
\[xy^{3}+y^{3}+3x^{2}-y+4 = 3x^{2}+y^{3}x+y^{3}-y+4\]
このとき、最も次数が高い項は \(3x^{2}\) で、その次数は \(2\) です。また、定数項は \(y^{3}-y+4\) です。
今回はこれで終わりです。この記事が気に入っていただけたら、SNS等でのシェアをよろしくお願いします!また、公式Xのフォローやブックマークなどもよろしくお願いします!