実数の大小
今回は絶対値について考えます。その前にまずは実数の大小について考えましょう。
それでは、実数の大小について数直線を用いて考えてみましょう。2つの実数を \(a, \ b\) として、数直線上の点 \(a\) が点 \(b\) より左側にあるとき、\(b\) が \(a\) より大きい、または \(a\) が \(b\) より小さいことを意味します。このことを
- \(b > a\) または \(a < b\)
と書きます。
ところで、数直線上の点 \(a\) に対して、点 \(b\) の位置は
- 点 \(a\) より左側
- 点 \(a\) と同じ位置
- 点 \(a\) より右側
のいずれかになります。このことを言い換えれば、2つの実数 \(a, \ b\) に対して、\(a < b, \quad a = b, \quad a > b\) の3つの関係のうちいずれか1つだけが成り立ちます。
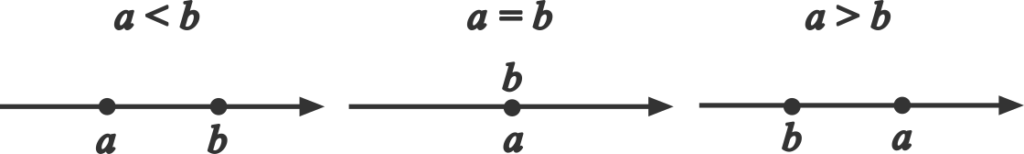
なお、\(a ≦ b\) は \(a\) が \(b\) より小さいかまたは等しいことを表し、\(a ≧ b\) は \(a\) が \(b\) より大きいかまたは等しいことを表します。
ここで少し話を変えて、実数の積について考えます。ご存知の通り、正の実数と正の実数の積は正の実数、負の実数と負の実数の積も正の実数になります。つまり、同じ符号の実数どうしの積は正の実数になります。このことから、0でない実数 \(a\) に対して \(a^{2}\) は常に正の実数になります。また、\(0^{2} = 0\) です。このことをまとめると以下のようになります。
実数 \(a\) に対して、常に \(a^{2} ≧ 0\) が成り立ち、\(a^{2} = 0\) となるのは \(a = 0\) のときに限る。
このことはぜひ頭に入れておいてください。
絶対値の定義
ここからはいよいよ絶対値について考えます。絶対値の定義は以下の通りです。
実数 \(a\) に対して、その絶対値 \(|a|\) は
\[|a| = \sqrt{a^{2}}\]
と定義される。
この定義はぜひ覚えてほしいのですが、より実用的な定義を紹介します。この定義は、上の定義と全く同じ意味をもちます。
実数 \(a\) に対して、その絶対値 \(|a|\) は
$$
|a| = \begin{cases}
a & (a ≧ 0) \\
-a & (a < 0)
\end{cases}
$$
と定義される。
すなわち、\(a\) が0以上ならば、その絶対値は \(a\) 自身で、\(a\) が0未満ならば、その絶対値は \(-a\) です。なお、絶対値は数から符号を取り除いたもの、と覚えている人は早めに上の定義に置き換えてください。今後は、この定義にしたがって絶対値を扱うことがとても重要になります。
また、定義から明らかに、常に \(|a| ≧ 0\) が成り立ち、\(|a|=0\) となるのは \(a=0\) のときに限ります。
ここで、絶対値の直感的(かつ本質的)な意味を説明します。絶対値 \(|a|\) は、数直線上の原点 \(O\) から点 \(a\) までの距離を表します。\(a\) を正の実数とすると、原点 \(O\) から点 \(a\) までの距離と、点 \(-a\) までの距離は等しいので、\(|a|=|-a|\) であることが確認できます。

絶対値の計算
それでは、絶対値の具体的な取り扱いについて確認します。絶対値を外す方法を例題で確認しましょう。
例題
場合分けをすることで \(|x-2|\) の絶対値記号を外してください。
解答・解説
絶対値記号のついた式は、場合分けをすることで絶対値記号を外すことができます。絶対値記号を外すときは、記号の中身が0以上か、0未満かで場合分けを行います。
絶対値記号の中身が0以上であることを数式で表すと、
\[x-2 ≧ 0\]
となります。この不等式を解くと、
\[x ≧ 2\]
です。これが、絶対値記号の中身が0以上となるような \(x\) の範囲です。同様に考えると、中身が0未満となるような \(x\) の範囲は \(x < 2\) であることが分かります。
絶対値記号の中身が0以上であれば、そのまま記号を外します。また、中身が0未満であれば、中身にマイナスをつけて記号を外します。よって答えは
$$
|x-2| = \begin{cases}
x-2 & (x ≧ 2) \\
-x+2 & (x < 2)
\end{cases}
$$
となります。

最後に、絶対値の積と商について紹介します。
\(a, \ b, \ c\) は実数で、\(c \neq 0\) とすると、
\(\quad \displaystyle |ab| = |a||b|\)
\(\displaystyle \quad \left|\frac{a}{c}\right| = \frac{|a|}{|c|}\)
が成り立つ。
証明
積のほうの式を証明してみます。
まず、\(|ab|\) の絶対値記号を外します。もちろん、
$$
|ab| = \begin{cases}
ab & (ab ≧ 0) \\
-ab & (ab < 0)
\end{cases}
$$
となります。
次に、\(|a||b|\) の絶対値記号を外します。場合分けは「\(a ≧ 0, \ b ≧ 0\)」「\(a ≧ 0, \ b < 0\)」「\(a < 0, \ b ≧ 0\)」「\(a < 0, \ b < 0\)」の4つなので、以下のように絶対値を外すことができます。
$$
|a||b| = \begin{cases}
ab & (a ≧ 0, \ b ≧ 0) \\
a(-b) & (a ≧ 0, \ b < 0) \\
(-a)b & (a < 0, \ b ≧ 0) \\
(-a)(-b) & (a < 0, \ b < 0)
\end{cases}
$$
ところで、\(a(-b) = (-a)b = -ab\) 、\((-a)(-b) = ab\) なので、\(|a||b| = ab\) となるのは \(a, \ b\) が同符号のときで、\(|a||b| = -ab\) となるのは \(a, \ b\) が異符号のときです。さらに、\(a, \ b\) が同符号であることは \(ab \ge 0\) であることに等しく、\(a, \ b\) が異符号であることは \(ab < 0\) であることに等しいです。よって、上の場合分けは下のように整理できます。
$$
|a||b| = \begin{cases}
ab & (ab ≧ 0) \\
-ab & (ab < 0)
\end{cases}
$$
これは \(|ab|\) の絶対値記号を外した式と等しいので、\(|ab| = |a||b|\) が証明できました。■
商の式も同様に証明できるので、ぜひやってみてください。
練習問題
問題
場合分けをすることで、以下の式の絶対値記号を外してください。
\((1) \quad |3x+2|\)
\((2) \quad |x-1||x+3|\)
\((3) \quad |x|+|x+2|\)
解答・解説
\((1)\)
\(3x+2 ≧ 0\)、すなわち \(\displaystyle x ≧ -\frac{2}{3}\) のとき、絶対値記号の中身は0以上なので、そのまま記号を外します。
\[|3x+2| = 3x+2\]
一方、\(3x+2 < 0\)、すなわち \(\displaystyle x < -\frac{2}{3}\) のとき、絶対値記号の中身は0未満なので、中身にマイナスをつけて記号を外します。
\[|3x+2| = -(3x+2) = -3x-2\]
よって答えは
$$ \displaystyle
|3x+2| = \begin{cases}
3x+2 & (x ≧ -\frac{2}{3}) \\
-3x-2 & (x < -\frac{2}{3})
\end{cases}
$$
となります。
\((2)\)
※この問題は2次不等式を解く必要があるので、分からない人は飛ばしてください。
絶対値の積の計算を使うと、
\[|x-1||x+3| = |(x-1)(x+3)|\]
となります。あとは同じように場合分けを行います。絶対値記号の中身が0以上となるのは、
- \((x-1)(x+3) ≧ 0\) すなわち \(x ≦ -3, \ 1 ≦ x\)
のときです。また、中身が0未満となるのは、
- \((x-1)(x+3) < 0\) すなわち \(-3 < x < 1\)
のときです。よって答えは
$$
|x-1||x+3| = \begin{cases}
(x-1)(x+3) & (x ≦ -3, \ 1 ≦ x) \\
-(x-1)(x+3) & (-3 < x < 1)
\end{cases}
$$
となります。
\((3)\)
絶対値記号が2つありますが、1つずつ考えれば大丈夫です。2つの絶対値記号をそれぞれ外すと、
$$
|x| = \begin{cases}
x & (x ≧ 0) \\
-x & (x < 0)
\end{cases}
$$
$$
|x+2| = \begin{cases}
x+2 & (x ≧ -2) \\
-x-2 & (x < -2)
\end{cases}
$$
となります。これをまとめていきます。
\(x < -2\) のとき \(|x| = -x, \ |x+2| = -x-2\) だから
\[|x|+|x+2| = -x+(-x-2) = -2x-2\]
\(-2 ≦ x < 0\) のとき \(|x| = -x, \ |x+2| = x+2\) だから
\[|x|+|x+2| = -x+(x+2) = 2\]
\(0 ≦ x\) のとき \(|x| = x, \ |x+2| = x+2\) だから
\[|x|+|x+2| = x+(x+2) = 2x+2\]
よって答えは
$$
|x|+|x+2| = \begin{cases}
2x+2 & (0 ≦ x) \\
2 & (-2 ≦ x < 0) \\
-2x-2 & (x < -2)
\end{cases}
$$
となります。
今回はこれで終わりです。この記事が気に入っていただけたら、SNS等でのシェアをよろしくお願いします!また、公式Xのフォローやブックマークなどもよろしくお願いします!
質問・感想等はぜひ下のコメント欄に書き込んでください!

