因数分解とは?
\(A, \ B\) を整式とするとき、\(A=BQ\) となるような整式 \(Q\) が存在するとき、\(B\) を \(A\) の因数といいます。そして、ある整式をいくつかの因数の積の形に表すことを、その整式の因数分解といいます。
簡単に言えば、ある整式をいくつかの(1次以上の)整式の積で表すことを、因数分解といいます。そして、積を作っている各式を因数といいます。
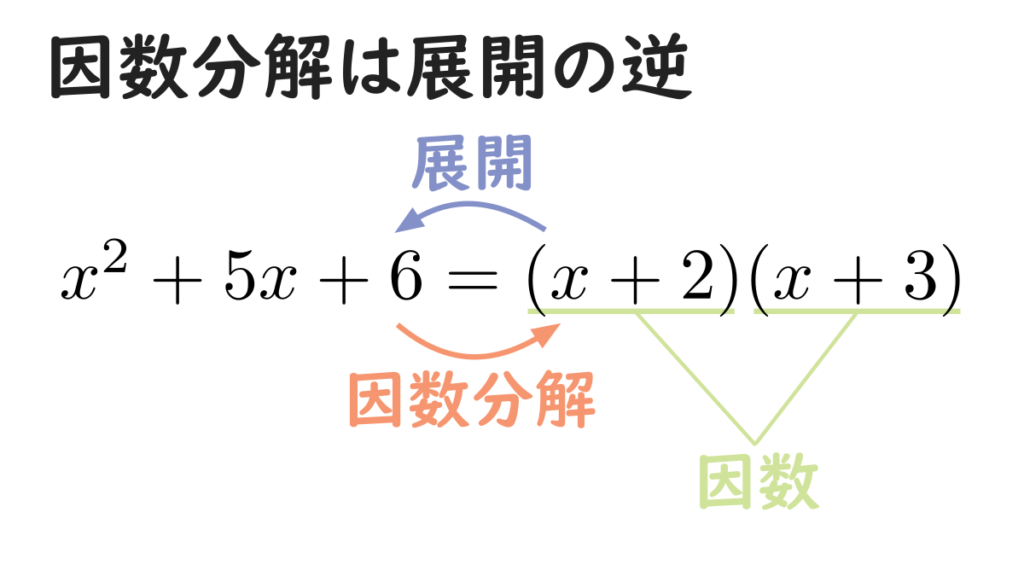
ところで、整式の積の形で表された式を単項式の和の形に表すことを、整式の展開といいましたね。よって、因数分解は展開の逆の操作であると言うことができます。
最も基本的な因数分解のやり方は、共通因数のくくり出しによる方法です。以下の例を見てください。
\begin{eqnarray}
2x^{2}+4x &=& 2x \cdot x+2x \cdot 2 \\[.5em]
&=& 2x(x+2)
\end{eqnarray}
この例では、\(2x^{2}+4x\) という整式の各項に \(2x\) という共通の因数が含まれているので、これをくくり出しました。その結果、\(2x(x+2)\) という籍の形に因数分解することができました。
整式を因数分解するときは、まず最初に共通因数のくくり出しが可能かどうかを試しましょう。
2次式の因数分解の公式
因数分解は展開の逆なので、展開の公式をそのまま因数分解に使うことができます。以下に2次式の因数分解の公式をまとめましたが、これらは2次式の展開公式と全く同じものです。よって、すでに展開公式を暗記している方は、新しく覚えるべきものは何もありません。
\((\mathrm{i}) \quad a^{2}+2ab+b^{2} = (a+b)^{2}\)
\((\mathrm{ii}) \quad a^{2}-2ab+b^{2} = (a-b)^{2}\)
\((\mathrm{iii}) \quad a^{2} – b^{2} = (a+b)(a-b)\)
\((\mathrm{iv}) \quad x^{2}+(a+b)x+ab = (x+a)(x+b)\)
\((\mathrm{v}) \quad acx^{2}+(ad+bc)x+bd = (ax+b)(cx+d)\)
これらの式の証明は以下の記事で紹介しているので、ぜひご覧ください。

それでは、実際に例題を通じて公式を使った因数分解を試してみましょう。
例題1
以下の式を因数分解してください。
\((1) \quad x^{2}+2x+1\)
\((2) \quad 4x^{2}-12x+9\)
\((3) \quad x^{2}-16\)
\((4) \quad x^{2}+3x+2\)
解答・解説
\((1)\)
公式 \((\mathrm{i}) \ a^{2}+2ab+b^{2} = (a+b)^{2}\) を使います。\(a=x, \ b=1\) として公式に当てはめると、
\begin{eqnarray}
x^{2}+2x+1 &=& x^{2}+2 \cdot x \cdot 1+1^{2} \\[.5em]
&=& (x+1)^{2}
\end{eqnarray}
となります。
\((2)\)
公式 \((\mathrm{ii}) \ a^{2}-2ab+b^{2} = (a-b)^{2}\) を使います。少し分かりにくいですが、\(a=2x, \ b=3\) として公式に当てはめると、
\begin{eqnarray}
4x^{2}-12x+9 &=& (2x)^{2}-2 \cdot 2x \cdot 3+3^{2} \\[.5em]
&=& (2x-3)^{2}
\end{eqnarray}
となります。
\((3)\)
公式 \((\mathrm{iii}) \ a^{2} – b^{2} = (a+b)(a-b)\) を使います。\(a=x, \ b=4\) として公式に当てはめると、
\begin{eqnarray}
x^{2}-16 &=& x^{2}-4^{2} \\[.5em]
&=& (x+4)(x-4)
\end{eqnarray}
となります。
\((4)\)
このような式を見たら、足して \(3\) 、掛けて \(2\) になるような2つの整数が無いか考えてみます。少し考えると、\(1\) と \(2\) の組み合わせが当てはまることが分かります。実際、\(1+2=3, \ 1 \times 2 = 2\) です。
よって、公式 \((\mathrm{iv}) \ x^{2}+(a+b)x+ab = (x+a)(x+b)\) を使うことができます。\(a=1, \ b=2\) として公式に当てはめると、
\begin{eqnarray}
x^{2}+3x+2 &=& x^{2}+(1+2)x+1 \cdot 2 \\[.5em]
&=& (x+1)(x+2)
\end{eqnarray}
となります。
ところで、この例題には公式 \((\mathrm{v})\) を使う問題がありませんでした。実は、公式 \((\mathrm{v})\) を使うにはちょっとしたテクニックが必要なのです。そのテクニックについてはこれから解説します。
たすき掛けによる因数分解
それでは、公式 \((\mathrm{v})\) を使うときに用いられるテクニック、通称「たすき掛け」について解説します。具体例で考えたほうが分かりやすいので、以下の例題を解きながら解説します。
例題2
\(2x^{2}+7x+6\) を因数分解してください。
解答・解説
2次の項に係数 \(2\) が付いています。このように、2次の項の係数が \(1\) でない場合には公式 \((\mathrm{v}) \ acx^{2}+(ad+bc)x+bd = (ax+b)(cx+d)\) を使うことが多いです。
それでは、たすき掛けのやり方を1ステップずつ解説します。
まずは、2次の項の係数と定数項を横に書き並べます。ここでは、\(2\) と \(6\) を並べて書きます。

次に、掛けて \(2\) となるような2つの整数の組み合わせを考えて、先ほど書いた \(2\) の下に縦に書き並べます。\(6\) についても同様に考えて、下に2つの整数を書き並べます。ここでは、\(2\) の下に \(1\) と \(2\) を、\(6\) の下に \(2\) と \(3\) をそれぞれ並べて書きます。なぜなら、\(1 \times 2=2, \ 2 \times 3=6\) となるからです。
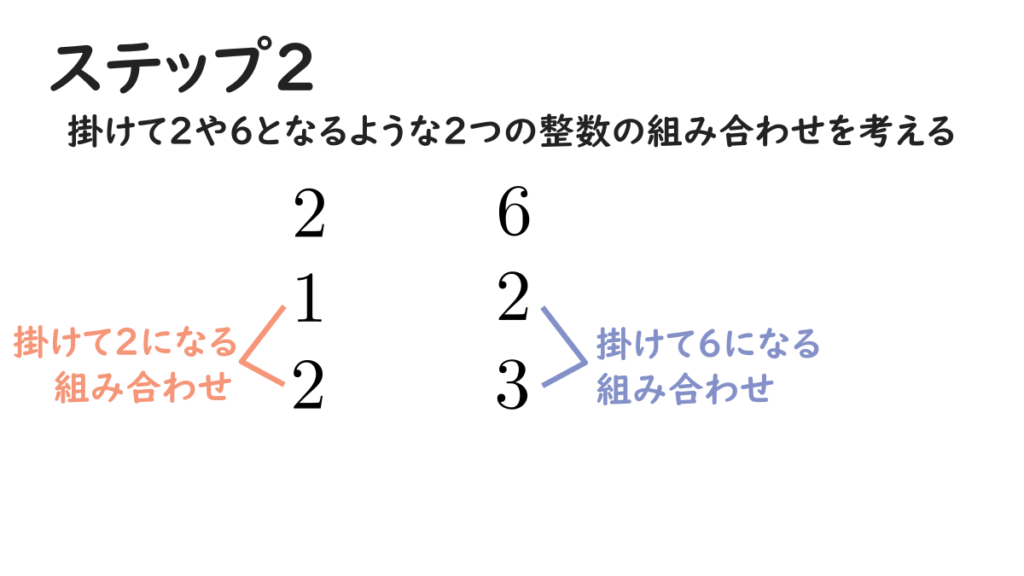
ここで、先ほど書き並べた4つの整数を、クロスするように掛け合わせます。掛け合わせた結果は右に書いておきます。
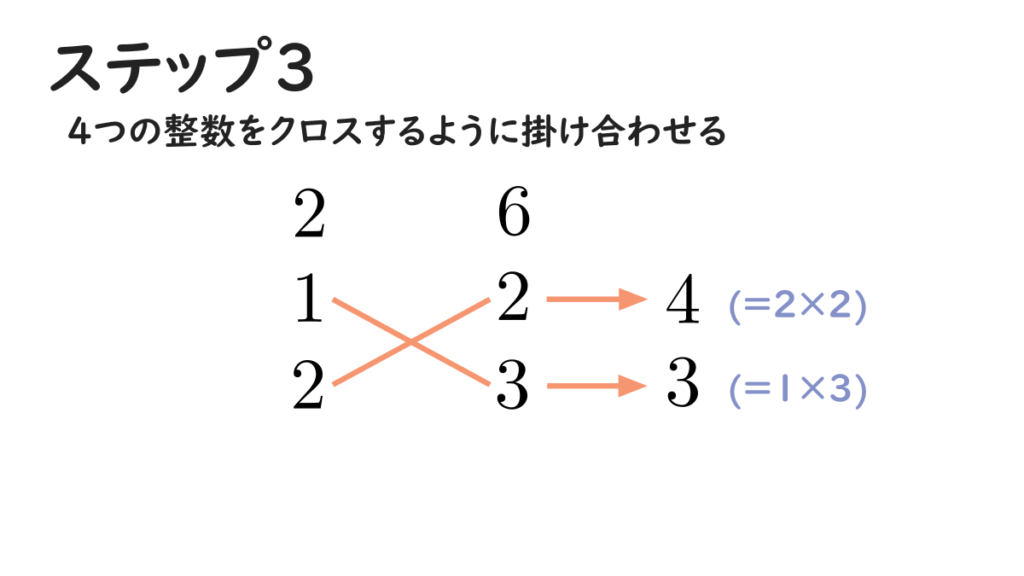
最後に、掛け合わせた結果として出てきた2つの整数を足し合わせて、その下に書きます。足し合わせた結果が1次の項の係数、つまり \(7\) と一致すれば成功です。
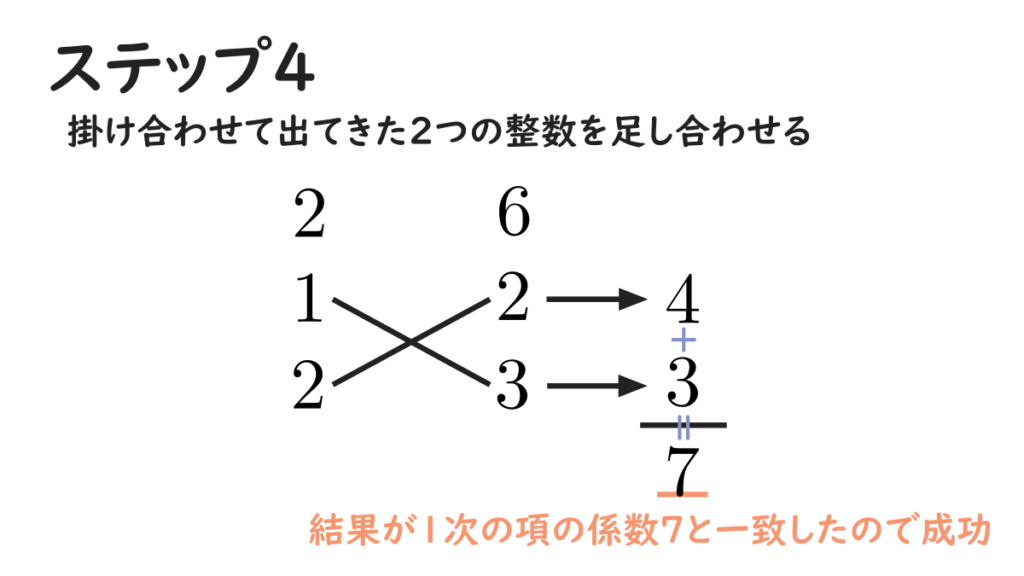
見事に結果が \(7\) となったので、あとは結果を式になおすだけです。クロスして掛け合わせた4つの数字のうち、左上を \(a\) 、右上を \(b\) 、左下を \(c\) 、右下を \(d\) とすると、因数分解の結果は \((ax+b)(cx+d)\) となります。よって答えは
\[2x^{2}+7x+6 = (x+2)(2x+3)\]
となります。

例題では一発で成功しましたが、実際には数字の組み合わせを何度も試行錯誤して、成功する組み合わせを見つけなければいけません。以下に、たすき掛けのやり方についてまとめました。
\(acx+(ad+bc)x+bd\) を因数分解する手順
- 2次の項の係数 \(ac\) と定数項 \(bd\) を横に書き並べる
- 掛けて \(ac\) となるような2つの整数 \(a, \ c\) 、掛けて \(bd\) となるような2つの整数 \(b, \ d\) を考えて、それぞれ下に書き並べる
- \(a \times d\) と \(b \times c\) を計算して、それらの結果を右に書く
- \(ad+bc\) を計算して、その結果を下に書く
- 4の結果が元の式の \(ad+bc\)(1次の項の係数)と一致するまで2~4を繰り返す
- 一致したときの \((ax+b)(cx+d)\) が計算結果となる

とはいえ、考えうるすべてのパターンを試すのは大変ですよね。そこでちょっとしたテクニックをお教えします。下の画像は、例題2で考えうるすべてのたすき掛けのパターンです。しかし、実はバツが付いているものは最初から考える必要はありません。
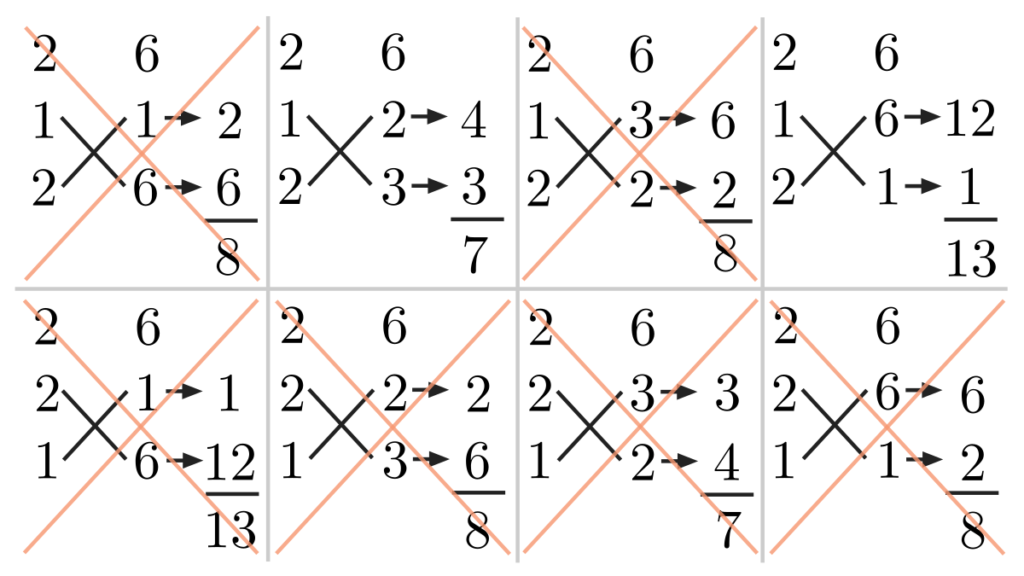
では、なぜこれらのパターンを考える必要がないのでしょうか?まず、下段の4つは上段の4つと同じ計算なので、考える必要はありません。
また、上段の2つも考える必要はありません。例えば、左上の例は式になおすと \((x+1)(2x+6)\) となりますが、これはさらに共通因数をくくり出して \(2(x+1)(x+3)\) とすることができます。これは、最初の式の時点で共通因数 \(2\) をくくり出せるということを意味していますが、最初の式 \(2x^{2}+7x+6\) から共通因数 \(2\) をくくり出すことはできません。よって、これらを考える必要はないのです。
簡単にまとめると、横に並んだ数字が約分できるような組み合わせのときは、たすき掛けを考える必要はないということです。例えば、左上の例では横に並んだ \(2\) と \(6\) は約分できる組み合わせなので、このようなたすき掛けを考える必要はありません。
ただし、因数分解しようとする式で共通因数のくくり出しができない場合に限ります。例えば、
\[4x^{2}+18x+8\]
のような式は、共通因数 \(2\) をくくり出すことができます。このような場合は、先に共通因数のくくり出しをしていないと、上のテクニックを使うことはできません。
3次式の因数分解の公式
ここからは3次式の因数分解の公式ですが、2次式のときと同様に、展開公式と全く同じ式となります。以下に3次式の因数分解の公式をまとめましたが、やはりすでに展開公式を暗記している方は、新しく覚えるべきことはありません。
\((\mathrm{vi}) \quad a^{3}+3a^{2}b+3ab^{2}+b^{3} = (a+b)^{3}\)
\((\mathrm{vii}) \quad a^{3}-3a^{2}b+3ab^{2}-b^{3} = (a-b)^{3}\)
\((\mathrm{viii}) \quad a^{3}+b^{3} = (a+b)(a^{2}-ab+b^{2})\)
\((\mathrm{ix}) \quad a^{3}-b^{3} = (a-b)(a^{2}+ab+b^{2})\)
例題を通じてこれらの公式を使った因数分解を試してみましょう。
例題3
以下の式を因数分解してください。
\((1) \quad x^{3}+6x^{2}+12x+8\)
\((2) \quad 8x^{3}-12x^{2}+6x-1\)
\((3) \quad x^{3}+27\)
\((4) \quad x^{3}-125\)
解答・解説
\((1)\)
公式 \((\mathrm{vi}) \ a^{3}+3a^{2}b+3ab^{2}+b^{3} = (a+b)^{3}\) を使います。\(a=x, \ b=2\) として公式に当てはめると、
\begin{align}
&x^{3}+6x^{2}+12x+8 \\[.5em]
&= x^{3}+3 \cdot x^{2} \cdot 2+3 \cdot x \cdot 2^{2}+2^{3} \\[.5em]
&= (x+2)^{3}
\end{align}
となります。
\((2)\)
公式 \((\mathrm{vii}) \ a^{3}-3a^{2}b+3ab^{2}-b^{3} = (a-b)^{3}\) を使います。\(a=2x, \ b=1\) として公式に当てはめると、
\begin{align}
&8x^{3}-12x^{2}+6x-1 \\[.5em]
&= (2x)^{3}-3 \cdot (2x)^{2} \cdot 1+3 \cdot 2x \cdot 1^{2}-1^{3} \\[.5em]
&= (2x-1)^{3}
\end{align}
となります。
\((3)\)
公式 \((\mathrm{viii}) \ a^{3}+b^{3} = (a+b)(a^{2}-ab+b^{2})\) を使います。\(a=x, \ b=3\) として公式に当てはめると、
\begin{eqnarray}
x^{3}+27 &=& x^{3}+3^{3} \\[.5em]
&=& (x+3)(x^{2}-3x+9)
\end{eqnarray}
となります。
\((4)\)
公式 \((\mathrm{ix}) \ a^{3}-b^{3} = (a-b)(a^{2}+ab+b^{2})\) を使います。\(a=x, \ b=5\) として公式に当てはめると、
\begin{eqnarray}
x^{3}-125 &=& x^{3}-5^{3} \\[.5em]
&=& (x-5)(x^{2}+5x+25)
\end{eqnarray}
となります。
練習問題
問題
以下の式を因数分解してください。
\((1) \quad x^{2}-4x\)
\((2) \quad x^{2}+x-12\)
\((3) \quad 4a^{2}-9b^{2}\)
\(\displaystyle (4) \quad x^{2}+x+\frac{1}{4}\)
\((5) \quad 4x^{2}+8x+3\)
\((6) \quad p^{3}+8q^{3}\)
\((7) \quad 2x^{4}-12x^{3}+24x^{2}-16x\)
\((8) \quad 6x^{2}-19x+10\)
解答・解説
\((1)\)
これは公式を使うのではなく、単に共通因数をくくり出すだけです。共通因数は \(x\) なので、
\[x^{2}-4x = x(x-4)\]
となります。
公式による因数分解に慣れると、共通因数のくくり出しを忘れがちになるので気をつけましょう。
\((2)\)
公式 \((\mathrm{iv}) \ x^{2}+(a+b)x+ab = (x+a)(x+b)\) を使います。
\begin{eqnarray}
x^{2}+x-12 &=& x^{2}+(4-3)x+4 \cdot (-3) \\[.5em]
&=& (x+4)(x-3)
\end{eqnarray}
\((3)\)
公式 \((\mathrm{iii}) \ a^{2} – b^{2} = (a+b)(a-b)\) を使います。
\begin{eqnarray}
4a^{2}-9b^{2} &=& (2a)^{2}-(3b)^{2} \\[.5em]
&=& (2a+3b)(2a-3b)
\end{eqnarray}
\((4)\)
分かりにくいですが、公式 \((\mathrm{i}) \ a^{2}+2ab+b^{2} = (a+b)^{2}\) を使うことができます。ここでは \(a=x, \ b=\frac{1}{2}\) となっています。
\begin{eqnarray}
x^{2}+x+\frac{1}{4} &=& x^{2}+2 \cdot x \cdot \frac{1}{2}+ \left( \frac{1}{2} \right) ^{2} \\[.5em]
&=& \left( x+\frac{1}{2} \right) ^{2}
\end{eqnarray}
\((5)\)
たすき掛けを用いて因数分解します。たすき掛けは以下の画像のようになります。
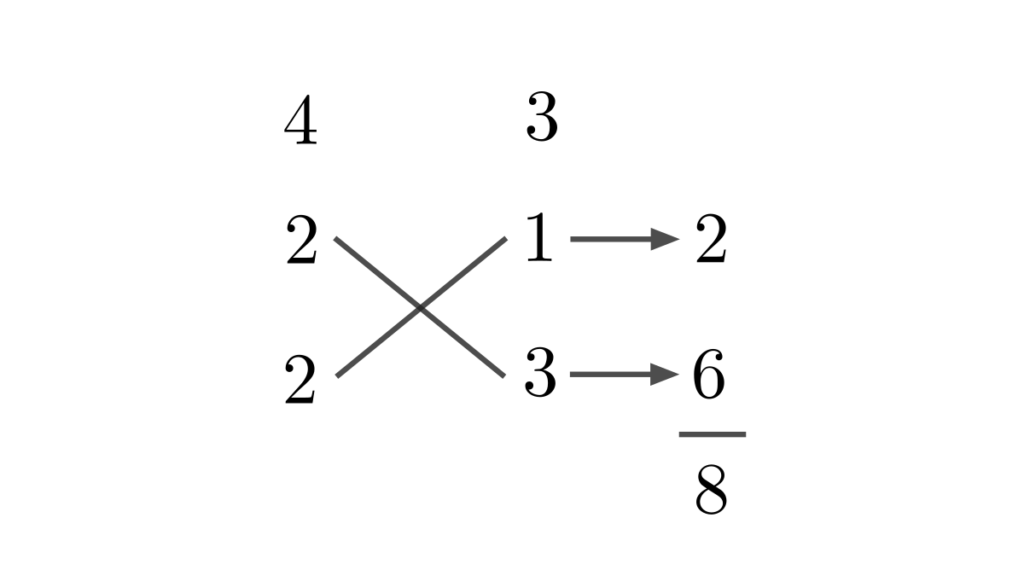
よって、因数分解の結果は
\[4x^{2}+8x+3 = (2x+1)(2x+3)\]
となります。
\((6)\)
公式 \((\mathrm{viii}) \ a^{3}+b^{3} = (a+b)(a^{2}-ab+b^{2})\) を使います。
\begin{eqnarray}
p^{3}+8q^{3} &=& p^{3}+(2q)^{3} \\[.5em]
&=& (p+2q)(p^{2}-2pq+4q^{2})
\end{eqnarray}
\((7)\)
4次式が出てきて驚いたかもしれませんが、まずは落ち着いて共通因数のくくり出しを行います。共通因数は \(2x\) なので、
\[2x^{4}-12x^{3}+24x^{2}-16x = 2x(x^{3}-6x^{2}+12x-8)\]
となります。
そうすると、公式 \((\mathrm{vii}) \ a^{3}-3a^{2}b+3ab^{2}-b^{3} = (a-b)^{3}\) が使えるようになるので、あとは公式を使って因数分解するだけです。実際に因数分解すると、
\begin{align}
&2x(x^{3}-6x^{2}+12x-8) \\[.5em]
&= 2x(x^{3}-3 \cdot x^{2} \cdot 2+3 \cdot x \cdot 2^{2}-2^{3}) \\[.5em]
&= 2x(x-2)^{3}
\end{align}
となります。
このように、一見して公式が使えなさそうな式でも、共通因数のくくり出しを行うことで、公式が使えるようになることがあります。
\((8)\)
たすき掛けを用いて因数分解しますが、この問題では負の整数まで考える必要があります。下の画像をご覧ください。
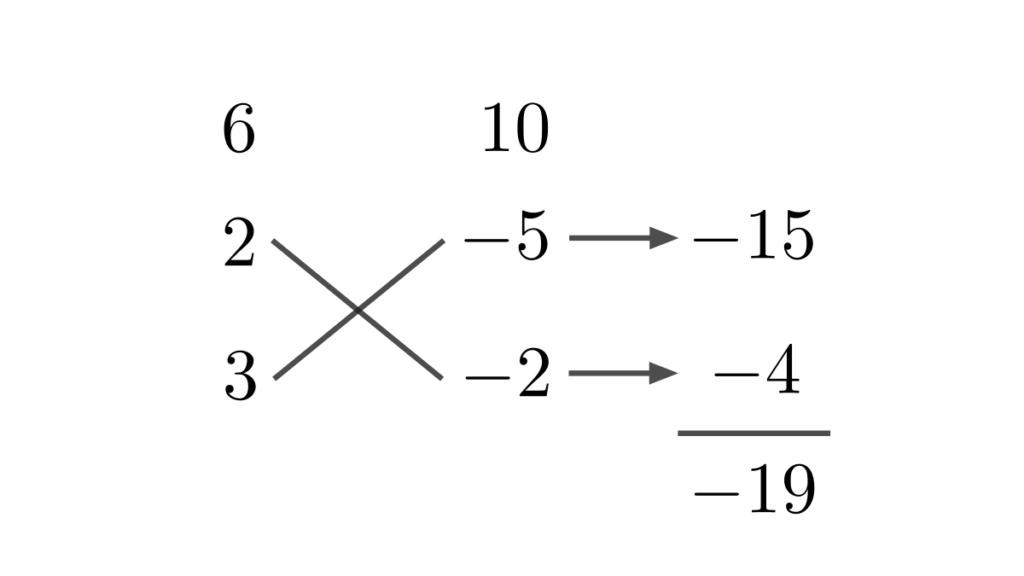
確かに、\((-5) \times (-2) = 10\) なので、このようなたすき掛けも考えることができますね。
上のたすき掛けの結果から、因数分解の結果は
\[6x^{2}-19x+10 = (2x-5)(3x-2)\]
となります。
この問題の式のように、係数や定数項に負の数が含まれている場合には、負の数のたすき掛けを考える必要があります。
因数分解に慣れないうちは、展開に比べて難しく感じるかもしれません。どの公式を使えばよいかすら分からないこともあるでしょうし、展開のように分配法則を使ってゴリ押しすることもできません。そのため、練習を積んで慣れていくしか方法はありません。高校数学を勉強し始めたばかりの皆さん、頑張ってください!
今回はこれで終わりです。この記事が気に入っていただけたら、SNS等でのシェアをよろしくお願いします!また、公式Xのフォローやブックマークなどもよろしくお願いします!
質問・感想等はぜひ下のコメント欄に書き込んでください!

