置き換えを利用した因数分解
今回は、因数分解を行うときに工夫が必要なパターンをいくつか紹介します。因数分解の公式など、因数分解の基礎に不安がある方は以下の記事をご覧ください。

今回は例題メインで解説していきます。早速、1つ目の例題を通じて置き換えを利用した因数分解を学びましょう。
例題1
以下の式を因数分解してください。
\((1) \quad (x+2)^{2}-2(x+2)-15\)
\((2) \quad x^{4}-8x^{2}+16\)
\((3) \quad a^{2}-b^{2}-2b-1\)
解答・解説
\((1)\)
\(x+2\) が繰り返し出てきているので、これを \(t\) とおきます。
\[(x+2)^{2}-2(x+2)-15 = t^{2}-2t-15\]
これで公式を使って因数分解することができるようになりました。因数分解を行うと、
\begin{eqnarray}
t^{2}-2t-15 &=& t^{2}+(3-5)x+3 \cdot (-5) \\[.5em]
&=& (t+3)(t-5)
\end{eqnarray}
となります。最後に、\(t=x+2\) を戻します。
\begin{eqnarray}
(t+3)(t-5) &=& (x+2+3)(x+2-5) \\[.5em]
&=& (x+5)(x-3)
\end{eqnarray}
\((2)\)
4次式ですが、4次の項・2次の項・定数項しかありません。このような場合は \(t=x^{2}\) とおくとうまくいきます。
\[x^{4}-8x^{2}+16 = t^{2}-8t+16\]
このように2次式となり、公式を使うことができるようになります。因数分解を行うと、
\begin{eqnarray}
t^{2}-8t+16 &=& t^{2}-2 \cdot t \cdot 4+4^{2} \\[.5em]
&=& (t-4)^{2}
\end{eqnarray}
となります。ここで \(t=x^{2}\) を戻すと、
\[(t-4)^{2} = (x^{2}-4)^{2}\]
となりますが、ここで計算を終わってはいけません。なぜなら、\(x^{2}-4\) がまだ因数分解できるからです。これを因数分解すると、
\begin{eqnarray}
(x^{2}-4)^{2} &=& (x^{2}-2^{2})^{2} \\[.5em]
&=& \{ (x+2)(x-2) \} ^{2} \\[.5em]
&=& (x+2)^{2}(x-2)^{2}
\end{eqnarray}
となります。
\((3)\)
この段階ではまだ置き換えを使うことができなさそうです。ひとまず因数分解できそうなところがないか探してみると、後半の \(-b^{2}-2b-1\) の部分が因数分解できそうです。実際に因数分解してみると、
\begin{eqnarray}
a^{2}-b^{2}-2b-1 &=& a^{2}-(b^{2}+2b+1) \\[.5em]
&=& a^{2}-(b^{2}+2 \cdot b \cdot 1+1^{2}) \\[.5em]
&=& a^{2}-(b+1)^{2}
\end{eqnarray}
となります。ここで \(t=b+1\) とおくと、
\[a^{2}-(b+1)^{2} = a^{2}-t^{2}\]
となります。さらに公式を使って因数分解を行います。
\[a^{2}-t^{2} = (a+t)(a-t)\]
最後に \(t=b+1\) を戻します。
\begin{eqnarray}
(a+t)(a-t) &=& (a+b+1) \{ a-(b+1) \} \\[.5em]
&=& (a+b+1)(a-b-1)
\end{eqnarray}

特定の文字に着目する
次に、複数の文字が含まれた式の因数分解のやり方を紹介します。キーワードは「特定の文字に着目する」です。例題を通じてその方法を確認しましょう。
例題2
以下の式を因数分解してください。
\((1) \quad x^{2}+xy+y-1\)
\((2) \quad a^{2}b+ab^{2}+b^{2}c+bc^{2}+c^{2}a+ca^{2}+2abc\)
\((3) \quad 3x^{2}+4xy-4y^{2}\)
解答・解説
\((1)\)
\(x, \ y\) の2つの文字が含まれており、このままだと因数分解が難しいので、特定の文字に着目します。
この式は2次式ですが、\(x\) に着目すると2次式、\(y\) に着目すると1次式です。このようなときは、次数が低い方の文字に着目します。\(y\) に着目して整理すると、
\[x^{2}+xy+y-1 = (x+1)y+x^{2}-1\]
となります。ここで、\(y\) に着目したときの定数項である \(x^{2}-1\) を因数分解すると、
\begin{eqnarray}
(x+1)y+x^{2}-1 &=& (x+1)y+x^{2}-1^{2} \\[.5em]
&=& (x+1)y+(x+1)(x-1)
\end{eqnarray}
となります。あとは、共通因数 \(x+1\) をくくり出して完了です。
\begin{eqnarray}
(x+1)y+(x+1)(x-1) &=& (x+1) \{ y+(x-1) \} \\[.5em]
&=& (x+1)(x+y-1)
\end{eqnarray}

\((2)\)
\(a, \ b, \ c\) の3つの文字が含まれており、このままだと因数分解が難しいので、特定の文字に着目します。
この式は3次式ですが、\(a, \ b, \ c\) のそれぞれに着目するとすべて2次式です。このように、どの文字に着目しても次数が同じときは、どの文字に着目しても大丈夫です。ここでは \(a\) に着目して整理すると、
\begin{align}
&a^{2}b+ab^{2}+b^{2}c+bc^{2}+c^{2}a+ca^{2}+2abc \\[.5em]
&= (b+c)a^{2}+(b^{2}+2bc+c^{2})a+b^{2}c+bc^{2}
\end{align}
となります。ここで、1次の項の係数 \(b^{2}+2bc+c^{2}\) と定数項 \(b^{2}c+bc^{2}\) を因数分解すると、
\begin{align}
&(b+c)a^{2}+(b^{2}+2bc+c^{2})a+b^{2}c+bc^{2} \\[.5em]
&= (b+c)a^{2}+(b+c)^{2}a+bc(b+c)
\end{align}
となります。次に、共通因数 \(b+c\) をくくり出します。
\[(b+c)a^{2}+(b+c)^{2}a+bc(b+c) = (b+c) \{ a^{2}+(b+c)a+bc \}\]
そうすると、\(a^{2}+(b+c)a+bc\) をさらに因数分解することができます。実際に因数分解すると、
\begin{eqnarray}
(b+c) \{ a^{2}+(b+c)a+bc \} &=& (b+c)(a+b)(a+c) \\[.5em]
&=& (a+b)(b+c)(c+a)
\end{eqnarray}
となります。
\((3)\)
この式は2次式ですが、\(x, \ y\) のそれぞれに着目しても2次式です。このようなときは、やはりどの文字に着目しても大丈夫です。ここでは \(x\) に着目して整理すると、
\[3x^{2}+4xy-4y^{2} = 3x^{2}+4yx-4y^{2}\]
となります(ほぼ変わっていませんが…)。ここで、たすき掛けを利用して因数分解を行います。たすき掛けは以下の画像のようになります。
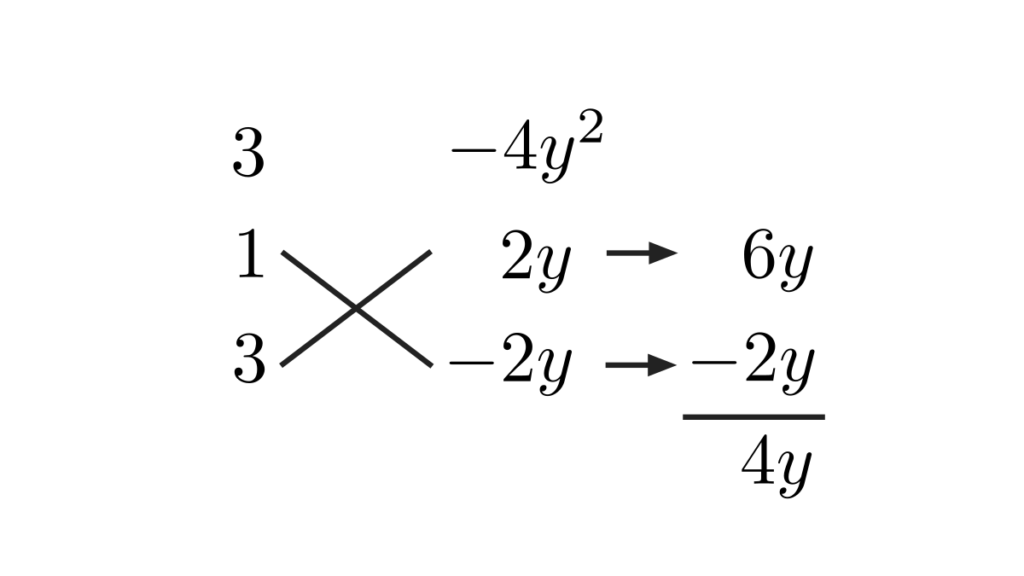
これを式になおすと、
\[3x^{2}+4yx-4y^{2} = (x+2y)(3x-2y)\]
となります。
なお、上のたすき掛けでは \(y\) をつけたまま行っていますが、\(y\) を考えずにたすき掛けを行い、あとから \(y\) をつけ加えても大丈夫です。
練習問題
問題
以下の式を因数分解してください。
\((1) \quad x^{2}+xy+5x+3y+6\)
\((2) \quad x^{2}-y^{2}+2x+1\)
\((3) \quad (a+b)^{3}+3(a+b)^{2}+3(a+b)+1\)
\((4) \quad x^{8}-2x^{4}-8\)
\((5) \quad 4x^{2}-11xy+6y^{2}\)
\((6) \quad p^{2}q-pq^{2}-q^{2}r+qr^{2}-r^{2}p-rp^{2}+2pqr\)
解答・解説
\((1)\)
\(x\) に着目すると2次式、\(y\) に着目すると1次式なので、\(y\) に着目して整理します。
\[x^{2}+xy+5x+3y+6 = (x+3)y+x^{2}+5x+6\]
そうすると、\(x^{2}+5x+6\) の部分が因数分解できそうなので、これを行います。
\begin{eqnarray}
(x+3)y+x^{2}+5x+6 &=& (x+3)y+x^{2}+(2+3)x+2 \cdot 3 \\[.5em]
&=& (x+3)y+(x+2)(x+3)
\end{eqnarray}
あとは共通因数 \(x+3\) をくくり出して完了です。
\begin{eqnarray}
(x+3)y+(x+2)(x+3) &=& (x+3)(y+x+2) \\[.5em]
&=& (x+3)(x+y+2)
\end{eqnarray}
\((2)\)
見やすいように項の順番を少し変えます。
\[x^{2}-y^{2}+2x+1 = x^{2}+2x+1-y^{2}\]
そうすると、\(x^{2}+2x+1\) の部分が因数分解できそうだ、ということに気づくと思います。実際に因数分解してみると、
\begin{eqnarray}
x^{2}+2x+1-y^{2} &=& x^{2}+2 \cdot x \cdot 1+1^{2}-y^{2} \\[.5em]
&=& (x+1)^{2}-y^{2}
\end{eqnarray}
となります。ここで \(t=x+1\) とおくと
\[(x+1)^{2}-y^{2} = t^{2}-y^{2}\]
となるので、公式を使って因数分解できそうですね。これを因数分解すると、
\[t^{2}-y^{2} = (t+y)(t-y)\]
となります。あとは \(t=x+1\) をもどして完了です。
\begin{eqnarray}
(t+y)(t-y) &=& (x+1+y)(x+1-y) \\[.5em]
&=& (x+y+1)(x-y+1)
\end{eqnarray}
\((3)\)
繰り返し出てくる \(a+b\) を \(t\) とおきます。
\[(a+b)^{3}+3(a+b)^{2}+3(a+b)+1 = t^{3}+3t^{2}+3t+1\]
ここで3次式の因数分解の公式を用いると、
\begin{eqnarray}
t^{3}+3t^{2}+3t+1 &=& t^{3}+3 \cdot t^{2} \cdot 1+3 \cdot t \cdot 1^{2}+1^{3} \\[.5em]
&=& (t+1)^{3}
\end{eqnarray}
となります。あとは \(t=a+b\) をもどすだけです。
\[(t+1)^{3} = (a+b+1)^{3}\]
\((4)\)
\(t=x^{4}\) とおきます。
\begin{eqnarray}
x^{8}-2x^{4}-8 &=& (x^{4})^{2}-2x^{4}-8 \\[.5em]
&=& t^{2}-2t-8
\end{eqnarray}
公式を用いて因数分解を行うと、
\begin{eqnarray}
t^{2}-2t-8 &=& t^{2}+(2-4)t+2 \cdot (-4) \\[.5em]
&=& (t+2)(t-4)
\end{eqnarray}
となります。ここで \(t=x^{4}\) をもどすと、
\[(t+2)(t-4) = (x^{4}+2)(x^{4}-4)\]
となります。しかし、ここで計算を終えてはいけません。まだ \(x^{4}-4\) を因数分解することができるからです。
\(u=x^{2}\) とおくと、
\begin{eqnarray}
(x^{4}+2)(x^{4}-4) &=& \{ (x^{2})^{2}+2 \} \{ (x^{2})^{2}-4 \} \\[.5em]
&=& (u^{2}+2)(u^{2}-4)
\end{eqnarray}
となり、\(u^{2}-4\) を因数分解することができます。
\begin{eqnarray}
(u^{2}+2)(u^{2}-4) &=& (u^{2}+2)(u^{2}-2^{2}) \\[.5em]
&=& (u^{2}+2)(u+2)(u-2)
\end{eqnarray}
あとは \(u=x^{2}\) をもどすだけです。
\begin{eqnarray}
(u^{2}+2)(u+2)(u-2) &=& \{ (x^{2})^{2}+2 \} (x^{2}+2)(x^{2}-2) \\[.5em]
&=& (x^{4}+2)(x^{2}+2)(x^{2}-2)
\end{eqnarray}
(有理数の範囲では)これ以上因数分解できないので、これで完了です。
なお、置き換えの計算に慣れてきたら、わざわざ文字でおかずに直接計算して大丈夫です。たとえば上の因数分解は、
\begin{eqnarray}
x^{8}-2x^{4}-8 &=& (x^{4}+2)(x^{4}-4) \\[.5em]
&=& (x^{4}+2)(x^{2}+2)(x^{2}-2)
\end{eqnarray}
のように計算することができます。
\((5)\)
\(x\) と \(y\) どちらに着目しても2次式なので、ここでは \(x\) に着目します。
\[4x^{2}-11xy+6y^{2} = 4x^{2}-11yx+6y^{2}\]
ここで、たすき掛けを用いて因数分解を行います。たすき掛けは以下の画像のようになります。
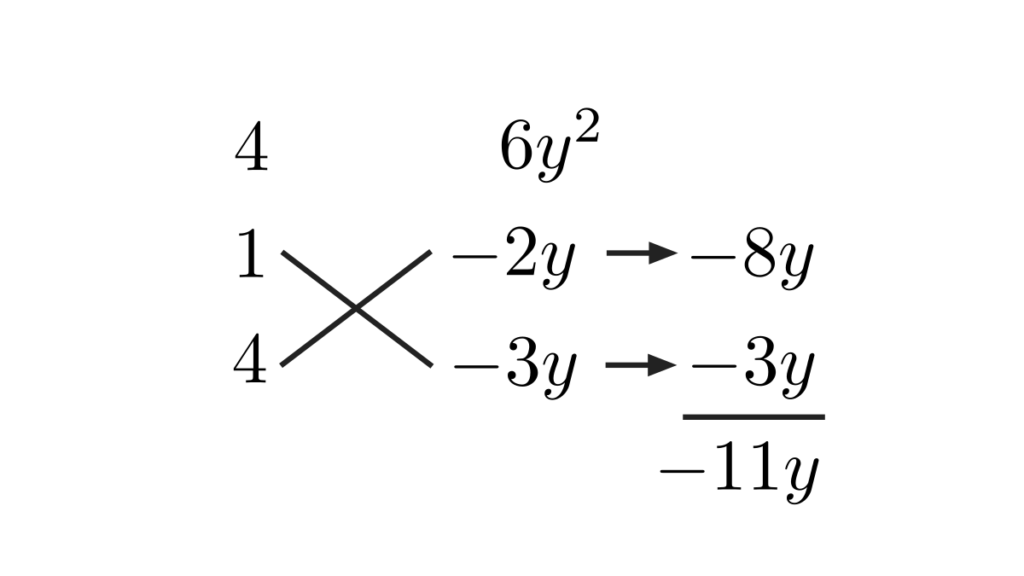
これを式になおすと、
\[4x^{2}-11yx+6y^{2} = (x-2y)(4x-3y)\]
となります。
\((6)\)
\(p, \ q, \ r\) のどれに着目しても2次式なので、ここでは \(p\) に着目します。
\begin{align}
&p^{2}q-pq^{2}-q^{2}r+qr^{2}-r^{2}p-rp^{2}+2pqr \\[.5em]
&= (q-r)p^{2}+(-q^{2}+2qr-r^{2})p-q^{2}r+qr^{2} \\[.5em]
&= (q-r)p^{2}-(q^{2}-2qr+r^{2})p-q^{2}r+qr^{2}
\end{align}
ここで、\(q^{2}-2qr+r^{2}, \ -q^{2}r+qr^{2}\) をそれぞれ因数分解すると、
\begin{align}
&(q-r)p^{2}-(q^{2}-2qr+r^{2})p-q^{2}r+qr^{2} \\[.5em]
&= (q-r)p^{2}-(q-r)^{2}p-qr(q-r)
\end{align}
となります。そうすると、共通因数 \(q-r\) をくくり出すことができます。
\begin{eqnarray}
(q-r)p^{2}-(q-r)^{2}p-qr(q-r) &=& (q-r) \{ p^{2}-(q-r)p-qr \} \\[.5em]
&=& (q-r) \{ p^{2}+(-q+r)p-qr \}
\end{eqnarray}
最後に、\(p^{2}+(-q+r)p-qr\) を因数分解して完了です。
\begin{eqnarray}
(q-r) \{ p^{2}+(-q+r)p-qr \} &=& (q-r)(p-q)(p+r) \\[.5em]
&=& (p-q)(q-r)(r+p)
\end{eqnarray}
今回はこれで終わりです。この記事が気に入っていただけたら、SNS等でのシェアをよろしくお願いします!また、公式Xのフォローやブックマークなどもよろしくお願いします!
質問・感想等はぜひ下のコメント欄に書き込んでください!

