1次不等式
不等式のすべての項を左辺に移項して整理したとき、
- \(ax+b>0\)
- \(ax+b≧0\)
- \(ax+b<0\)
- \(ax+b≦0\)
のいずれかの形になる不等式を、\(x\) の1次不等式といいます。左辺が1次式だから”1次”不等式です。
1次不等式は、不等式の性質を用いて簡単に解くことができます。不等式のさまざまな性質については、以下の記事で詳しく解説しているので、ぜひご覧ください。

1次不等式は、以下のような手順で機械的に解くことができます。
1次不等式 \(ax+b>0\) を解く手順は、
- 定数項 \(b\) を移項して \(ax>-b\) の形にする。
- 両辺を \(x\) の係数 \(a\) で割る。\(a<0\) のときは不等号の向きが変わることに注意。
もちろん、\(ax+b>0\) だけでなく、\(ax+b≧0\) 、\(ax+b<0\) 、\(ax+b≦0\) なども同様の手順で解くことができます。
さっそく、1次不等式の解き方を例題で確認しましょう。
例題
以下の不等式を解いてください。
\((1) \quad 2x-6>0\)
\((2) \quad -6a+9≦0\)
\((3) \quad 3x+7<8\)
\((4) \quad x+6≧3x-4\)
解答・解説
\((1)\)
手順に沿って解いていきます。まずは定数項 \(-6\) を右辺に移項して、
\[2x>6\]
次に両辺を \(x\) の係数 \(2\) で割って、
\[x>3\]
\(2>0\) なので不等号の向きは変わりません。
(答)\(x>3\)
\((2)\)
これも手順に沿って解いていきます。まずは定数項 \(9\) を右辺に移項して、
\[-6a≦-9\]
次に両辺を \(a\) の係数 \(-6\) で割ります。\(-6<0\) なので不等号の向きが変わることに注意して、
\[a≧\frac{3}{2}\]
となります。
(答)\(\displaystyle a≧\frac{3}{2}\)
\((3)\)
これまでと少し形が違いますが、\(ax>-b\) の形を目指すことは変わりません。左辺の \(7\) を右辺に移項して、
\[3x<8-7\]
\[3x<1\]
次に両辺を \(x\) の係数 \(3\) で割って、
\[x<\frac{1}{3}\]
\(3>0\) なので不等号の向きは変わりません。
(答)\(\displaystyle x<\frac{1}{3}\)
\((4)\)
これもやはり \(ax>-b\) の形を目指すことに変わりありません。左辺の \(6\) を右辺に、右辺の \(3x\) を左辺に移項して、
\[x-3x≧-4-6\]
\[-2x≧-10\]
次に両辺を \(x\) の係数 \(-2\) で割りますが、\(-2<0\) なので不等号の向きが変わることに注意して、
\[x≦5\]
となります。
(答)\(x≦5\)
例題を通じて気付いたかもしれませんが、1次不等式の解き方は1次方程式とほとんど変わりません。ただし、両辺に負の数を掛けたり、負の数で割ったりするときに不等号の向きが変わることに注意が必要です。

不等式の解とは?
ここからは少し余談になりますが、不等式の解の意味について少し考えてみましょう。
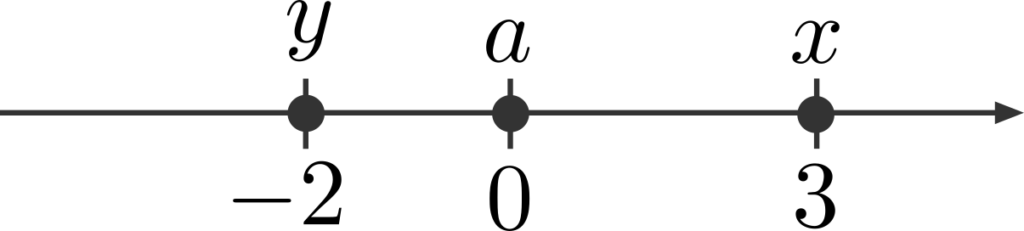
まず、1次方程式の解について振り返りましょう。1次方程式の解は、
- \(x=3\)
- \(y=-2\)
- \(a=0\)
のように、1つの数で表されます。これを数直線に表すと、以下のように1つの点で表されます。
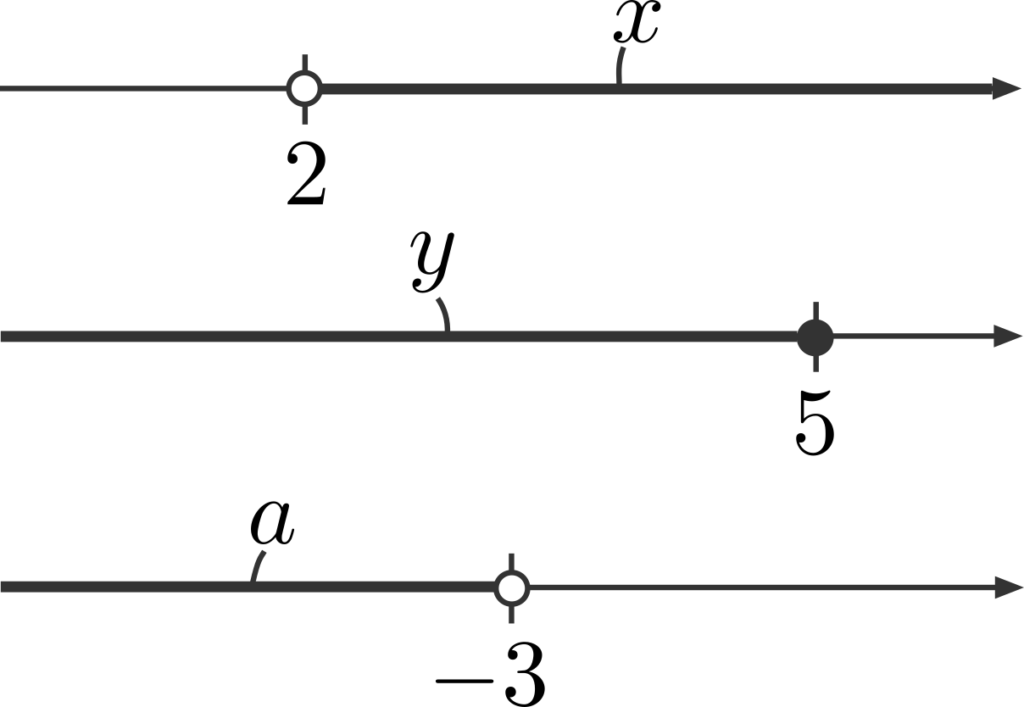
では、1次不等式の解はどうでしょうか。1次不等式の解は、
- \(x>2\)
- \(y≦5\)
- \(a<-3\)
のように、1つの範囲で表されます。数直線上では以下のように表されます。黒い点はその点を含むことを、白い点はその点を含まないことを表します。
上のことを言い換えれば、数直線上のある範囲に存在するすべての実数が不等式の解になります。もちろん、そのような実数は無数に存在しています。すなわち、不等式の解とは、不等式を満たすような(多くの場合は無数に存在する)すべての実数を、ある範囲として表したものです。
練習問題
問題
以下の不等式を解いてください。
\((1) \quad 3x+7<0\)
\((2) \quad 2-p>2p-1\)
\(\displaystyle (3) \quad \frac{x}{2}≧\frac{2}{3}-x\)
\((4) \quad -4x<0\)
\(\displaystyle (5) \quad \frac{x+3}{9}>\frac{x+2}{3}\)
\(\displaystyle (6) \quad \sqrt{2}x-4≦2\sqrt{3}\)
解答・解説
\((1)\)
\[3x<-7\]
\[x<-\frac{7}{3}\]
(答)\(\displaystyle x<-\frac{7}{3}\)
\((2)\)
\[-p-2p>-1-2\]
\[-3p>-3\]
両辺を \(-3\) で割ると不等号の向きが変わることに注意して
\[p<1\]
(答)\(p<1\)
\((3)\)
分数が含まれていると計算が面倒なので、方程式を解くときと同様に、両辺に \(6\) を掛けます。
\[\frac{x}{2} \times 6≧\left( \frac{2}{3}-x\right) \times 6\]
\[3x≧4-6x\]
あとはこれまでと同様に解くだけです。
\[3x+6x≧4\]
\[9x≧4\]
\[x≧\frac{4}{9}\]
(答)\(\displaystyle x≧\frac{4}{9}\)
\((4)\)
両辺を \(-4\) で割るだけですが、不等号の向きが変わることに注意しましょう。
\[x>0\]
(答)\(x>0\)
\((5)\)
両辺に \(9\) を掛けます。
\[\frac{x+3}{9} \times 9>\frac{x+2}{3} \times 9\]
\[x+3>3(x+2)\]
\[x+3>3x+6\]
あとは手順通りにに解くだけです。
\[x-3x>6-3\]
\[-2x>3\]
\[x<-\frac{3}{2}\]
(答)\(\displaystyle x<-\frac{3}{2}\)
\((6)\)
無理数が含まれていても気にせずに解きましょう。
\[\sqrt{2}x≦2\sqrt{3}+4\]
\[x≦\frac{2\sqrt{3}+4}{\sqrt{2}}\]
最後に分母を有理化しておきます。
\[x≦\sqrt{6}+2\sqrt{2}\]
(答)\(\displaystyle x≦\sqrt{6}+2\sqrt{2}\)
今回はこれで終わりです。この記事が気に入っていただけたら、SNS等でのシェアをよろしくお願いします!また、公式Xのフォローやブックマークなどもよろしくお願いします!
質問・感想等はぜひ下のコメント欄に書き込んでください!

