整式の加法・減法
整式の加法・減法のやり方は簡単です。ただ項を書き並べて、同類項の整理をするだけです。なお、同類項を整理する方法は、以下の記事で解説しています。ぜひご覧ください。
さっそく、例題で整式の加法・減法のやり方を確認しましょう。
例題1
\(A = 2x^{2}+3x-4, \ B = 5x^{2}-x+2\) とするとき、\(A+B, \ A-B\) を計算をしてください。
解答・解説
まずは、\(A+B\) の \(A, \ B\) の部分にそれぞれ \(2x^{2}+3x-4, \ 5x^{2}-x+2\) を代入します。
\[A+B = (2x^{2}+3x-4)+(5x^{2}-x+2)\]
あとは、カッコを外して同類項をまとめるだけです。
\begin{align}
&(2x^{2}+3x-4)+(5x^{2}-x+2) \\[0.5em]
&= 2x^{2}+3x-4+5x^{2}-x+2 \\[0.5em]
&= (2+5)x^{2}+(3-1)x+(-4+2) \\[0.5em]
&= 7x^{2}+2x-2
\end{align}
よって、 \(A+B=7x^{2}+2x-2\) と計算できました。
次に、\(A-B\) を計算しましょう。足し算と同様に、まずは \(A-B\) に \(A = 2x^{2}+3x-4, \ B = 5x^{2}-x+2\) を代入します。
\[A-B = (2x^{2}+3x-4)-(5x^{2}-x+2)\]
あとはカッコを外して同類項をまとめるだけですが、引き算の場合にはカッコを外すときに注意が必要です。\(-( \ )\) という形のカッコを外すときには、カッコの中の符号をすべて反転させます。
\begin{align}
&(2x^{2}+3x-4)-(5x^{2}-x+2) \\[0.5em]
&= 2x^{2}+3x-4-5x^{2}+x-2 \\[0.5em]
&= (2-5)x^{2}+(3+1)x+(-4-2) \\[0.5em]
&= -3x^{2}+4x-6
\end{align}
よって、 \(A-B=-3x^{2}+4x-6\) と計算できました。
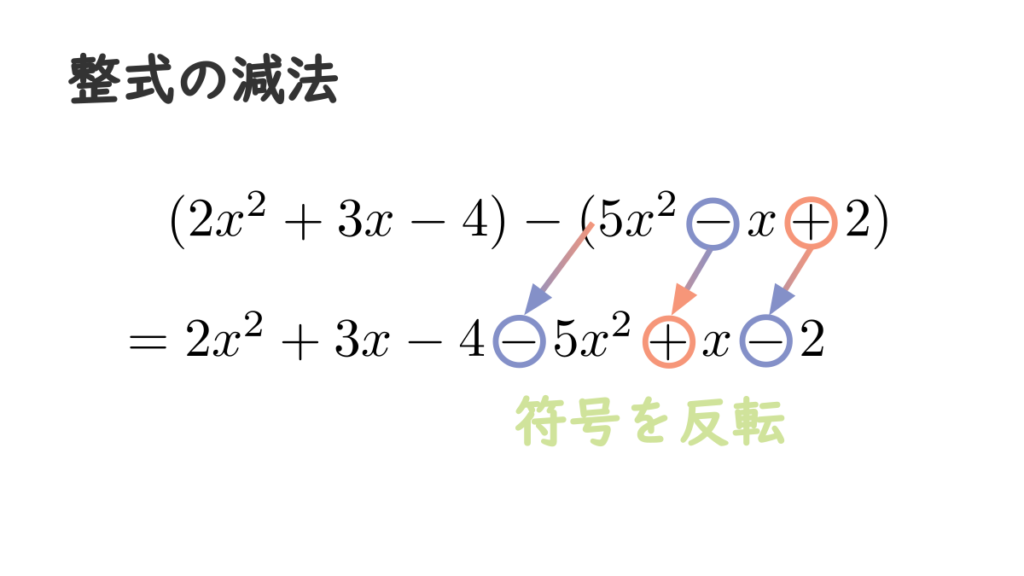
なお、以下のように縦に書き並べて、筆算で計算することもできます。
\begin{align}
\phantom{+\big{)}} \ 2x^{2}+3x-4 \\
\rlap{\underline{\phantom{+ \big{)} 2x^{2}+3x-400}}} + \big{)} \ 5x^{2}-\phantom{0}x+2 \\
\phantom{+\big{)}} \ 7x^{2}+2x-2
\end{align}
\begin{align}
\phantom{-\big{)}} \ 2x^{2}+3x-4 \\
\rlap{\underline{\phantom{- \big{)} 2x^{2}+3x-400}}} – \big{)} \ 5x^{2}-\phantom{0}x+2 \\
\phantom{-\big{)}}-3x^{2}+4x-6
\end{align}
整式の計算の基本法則
ここで、整式の加法・乗法において成り立つ法則を紹介します。
\(A, \ B, \ C\) を整式とする。
交換法則
\[A+B=B+A, \quad AB=BA\]
結合法則
\[(A+B)+C=A+(B+C), \quad (AB)C=A(BC)\]
分配法則
\[A(B+C)=AB+AC, \quad (A+B)C=AC+BC\]
このように、整式の加法・乗法には、実数と同じような交換法則・結合法則・分配法則が成り立ちます。
また、整式には単項式と多項式が含まれるので、整式 \(A, \ B, \ C\) は単項式でも多項式でも大丈夫です。すなわち、多項式どうしだけではなく、単項式どうしや単項式と多項式の間にも上の法則が成り立ちます。
なお、整式の数を増やしても、上と同様の法則が成り立ちます。例えば、
\[A(B+C+D)=AB+AC+AD\]
のような等式も成り立ちます。
整式の乗法
整式の乗法には、上で紹介した分配法則と、指数法則を使います。
整式の乗法のやり方については、以下の例題で確認しましょう。
例題2
以下の式を、単項式の和の形にしてください。
\[(1) \quad 3x(x^{2}+4x)\]
\[(2) \quad x^{2}(2x^{3}-x+3)\]
\[(3) \quad (x^{2}+4)(3x-2)\]
解答・解説
\((1)\)
まずは単項式と多項式の積です。分配法則 \(A(B+C)=AB+AC\) を用いて計算すると
\begin{align}
&3x(x^{2}+4x) \\[0.5em]
&= 3x \cdot x^{2} + 3x \cdot 4x
\end{align}
となります。なお、記号”\(\cdot\)”は積の記号で、”\(\times\)”と同じ意味です。
あとは、指数法則 \(a^{m}a^{n}=a^{m+n}\) を使って計算しましょう。
\begin{align}
&3x \cdot x^{2} + 3x \cdot 4x \\[0.5em]
&= 3 x^{1+2} + 3 \cdot 4x^{1+1} \\[0.5em]
&= 3x^{3} + 12x^{2}
\end{align}
よって、\(3x(x^{2}+4x)=3x^{3} + 12x^{2}\) と計算できました。
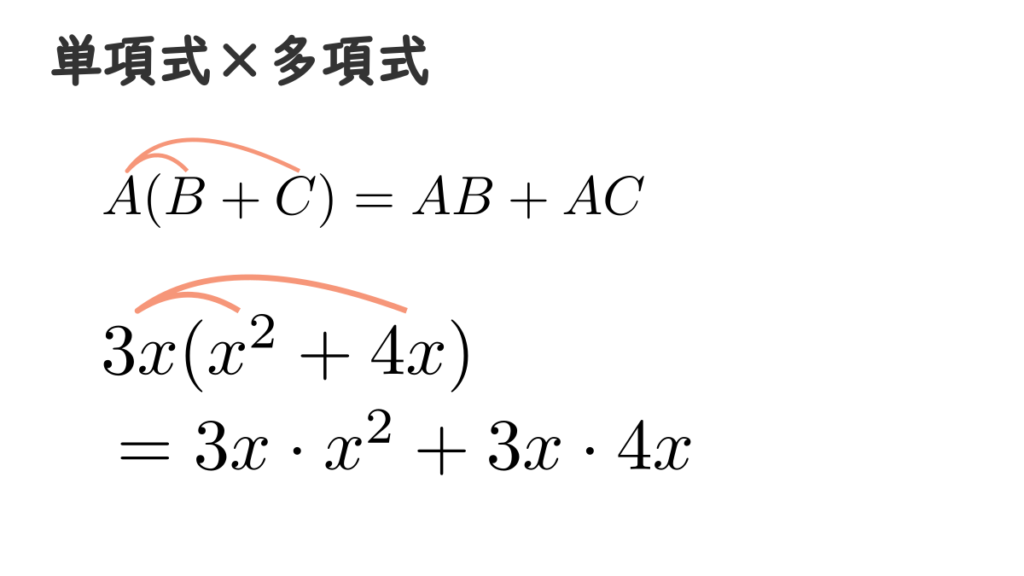
\((2)\)
次も単項式と多項式の積ですが、項の数が増えています。ここでは、\(A(B+C+D)=AB+AC+AD\) を用いて計算しましょう。
\begin{align}
&x^{2}(2x^{3}-x+3) \\[0.5em]
&= x^{2} \cdot 2x^{3} + x^{2} \cdot (-x) + x^{2} \cdot 3 \\[0.5em]
&= 2x^{2+3} – x^{2+1} + 3x^{2} \\[0.5em]
&= 2x^{5} – x^{3} + 3x^{2}
\end{align}
よって、\(x^{2}(2x^{3}-x+3)=2x^{5} – x^{3} + 3x^{2}\) と計算できました。
\((3)\)
最後は多項式どうしの積です。このような場合は、分配法則を複数回に分けて使います。まずは、\(A=x^{2}+4, \ B=3x, \ C=-2\) として分配法則 \(A(B+C)=AB+AC\) を使いましょう。
\begin{align}
&(x^{2}+4)(3x-2) \\[0.5em]
&= (x^{2}+4)3x + (x^{2}+4)(-2)
\end{align}
すると、分配法則 \((A+B)C=AC+BC\) を使うことができる形が2つ出てきました。\((x^{2}+4)3x, \ (x^{2}+4)(-2)\) にそれぞれ分配法則 \((A+B)C=AC+BC\) を用いると
\begin{align}
&(x^{2}+4)3x + (x^{2}+4)(-2) \\[0.5em]
&= x^{2} \cdot 3x + 4 \cdot 3x + x^{2} \cdot (-2) + 4 \cdot (-2) \\[0.5em]
&= 3x^{3} + 12x – 2x^{2} -8 \\[0.5em]
&= 3x^{3} – 2x^{2} + 12x -8
\end{align}
最後は降べきの順に整理しました。よって、\((x^{2}+4)(3x-2)=3x^{3} – 2x^{2} + 12x -8\) です。

上の例題のように整式の積で表された式を、単項式の和の形、すなわち1つの整式にする計算を、整式の展開といいます。
練習問題
問題
整式 \(X, \ Y\) を
\[X=x^{2}+3\]
\[Y=-5x+2x^{2}+6\]
とするとき、以下の計算をしてください。結果は単項式の和の形とし、降べきの順に整理してください。
\[(1) \quad X+Y\]
\[(2) \quad X-Y\]
\[(3) \quad XY\]
解答・解説
整式どうしの演算をするときは、すべての整式を降べきの順に整理しておくと計算がしやすくなります。ここでは、\(Y\) を降べきの順に整理しましょう。
\begin{eqnarray}
Y &=& -5x+2x^{2}+6 \\[0.5em]
&=& 2x^{2}-5x+6
\end{eqnarray}
\((1)\)
単なる同類項の整理です。
\begin{eqnarray}
X+Y &=& (x^{2}+3)+(2x^{2}-5x+6) \\[0.5em]
&=& x^{2}+3+2x^{2}-5x+6 \\[0.5em]
&=& 3x^{2}-5x+9
\end{eqnarray}
よって、\(X+Y=3x^{2}-5x+9\) です。
筆算で計算する場合は以下のようになります。欠けている項は空白として、上下に同類項が並ぶようにします。
\begin{align}
\phantom{+\big{)}} \ \phantom{2}x^{2}\phantom{-5x}+3 \\
\rlap{\underline{\phantom{+ \big{)} \ x^{2}\phantom{-5x}+3000}}} + \big{)} \ 2x^{2}-5x+6 \\
\phantom{+\big{)}} \ 3x^{2}-5x+9
\end{align}
\((2)\)
これも単純な同類項の整理です。ただし、\(-( \ )\) という形のカッコを外すときに、カッコの中の符号をすべて反転させることに注意しましょう。
\begin{eqnarray}
X-Y &=& (x^{2}+3)-(2x^{2}-5x+6) \\[0.5em]
&=& x^{2}+3-2x^{2}+5x-6 \\[0.5em]
&=& -x^{2}+5x-3
\end{eqnarray}
よって、\(X-Y=-x^{2}+5x-3\) です。
筆算で計算する場合は以下のようになります。
\begin{align}
\phantom{+\big{)}} \ \phantom{2}x^{2}\phantom{-5x}+3 \\
\rlap{\underline{\phantom{- \big{)} \ x^{2}\phantom{-5x}+3000}}} – \big{)} \ 2x^{2}-5x+6 \\
\phantom{+\big{)}} \ -x^{2}+5x-3
\end{align}
\((3)\)
最後は多項式どうしの乗算です。分配法則を複数回使って計算します。まずは \((A+B)C=AC+BC\) を使います。
\begin{eqnarray}
XY &=& (x^{2}+3)(2x^{2}-5x+6) \\[0.5em]
&=& x^{2}(2x^{2}-5x+6)+3(2x^{2}-5x+6)
\end{eqnarray}
次に、\(A(B+C+D)=AB+AC+AD\) を2か所で使って展開します。
\begin{align}
&x^{2}(2x^{2}-5x+6)+3(2x^{2}-5x+6) \\[0.5em]
&= x^{2} \cdot 2x^{2} + x^{2} \cdot (-5x) + x^{2} \cdot 6 + 3 \cdot 2x^{2} + 3 \cdot (-5x) + 3 \cdot 6 \\[0.5em]
&= 2x^{4}-5x^{3}+6x^{2}+6x^{2}-15x+18 \\[0.5em]
&= 2x^{4}-5x^{3}+12x^{2}-15x+18
\end{align}
よって、\(XY=2x^{4}-5x^{3}+12x^{2}-15x+18\) です。
慣れてきたら、はじめから以下のように展開しましょう。
\begin{align}
&(x^{2}+3)(2x^{2}-5x+6) \\[0.5em]
&= x^{2} \cdot 2x^{2} + x^{2} \cdot (-5x) + x^{2} \cdot 6 + 3 \cdot 2x^{2} + 3 \cdot (-5x) + 3 \cdot 6
\end{align}
今回はこれで終わりです。この記事が気に入っていただけたら、SNS等でのシェアをよろしくお願いします!また、公式Xのフォローやブックマークなどもよろしくお願いします!