有理数・無理数
数にはいろいろな種類があります。今回は、そのうちの実数について詳しく見ていきましょう。
まずは整数についてです。\(0, \ 1, \ -1, \ 2, \ -2, \ \cdots\) のような数を整数といいます。そのうち、\(1, \ 2, \ 3, \ \cdots\) を正の整数(自然数)、\(-1, \ -2, \ -3, \ \cdots\) を負の整数といいます。\(0\) は正でも負でもない整数です。
次は有理数についてです。有理数については、以下の定義をしっかり覚えましょう。
有理数とは、整数を \(m\) 、自然数を \(n\) として、
\[\frac{m}{n}\]
の形に表される数である。
つまり、
\[\frac{2}{5}, \ \frac{-25}{3}, \ \frac{1}{3}\]
のような数が有理数です。
また、任意の整数 \(m\) は \(\frac{m}{1}\) の形に表せるので、整数は有理数です。
最後は無理数についてです。無理数とは、有理数でない実数のことです。例えば、
\[\sqrt{2}, \ -\frac{\sqrt{3}}{5}, \ \pi\]
のような数が無理数です。
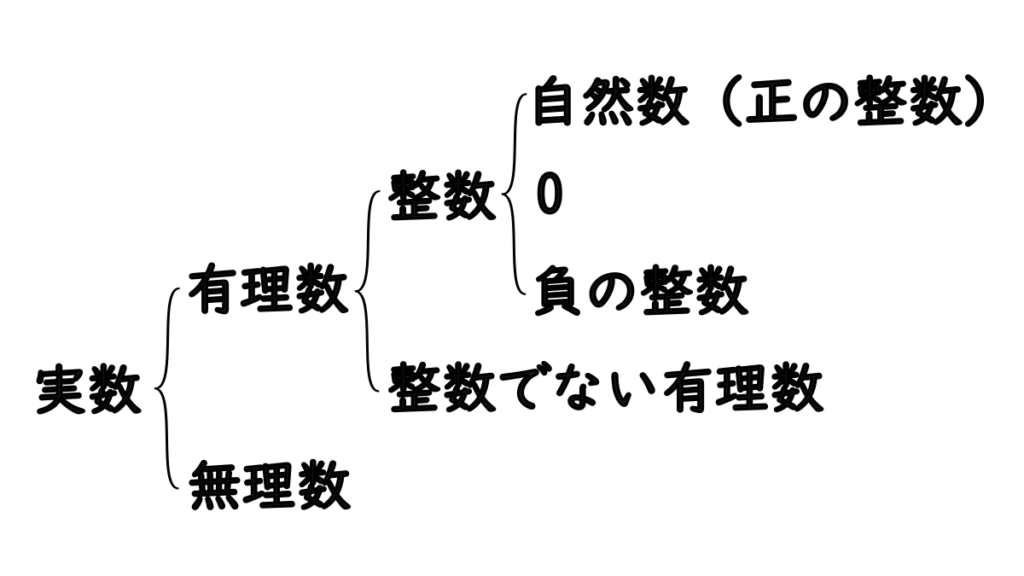
以上のことをまとめると、実数は以下の画像のように分類することができます。この図はよく頭に入れておきましょう。
実数を小数で表す
実数は小数で表すことができます。整数でない有理数を小数で表すと、以下の例のようになります。
\begin{eqnarray}
\frac{1}{4} &=& 0.25 \\[0.5em]
-\frac{2}{3} &=& 0.666\cdots \\[0.5em]
\frac{322}{1665} &=& 0.1933933933\cdots
\end{eqnarray}
\(0.25\) のような割り切れる小数を有限小数といいます。一方、\(0.666\cdots\) や \(0.1933933933\cdots\) のように、小数点以下が無限に続く小数を無限小数といいます。特に、上の例のように、ある位以下に同じ数字の並びが繰り返される無限小数を循環小数といいます。
例えば、\(0.666\cdots\) という循環小数は小数第1位以下に \(6\) という数字が繰り返されています。また、\(0.1933933933\cdots\) という循環小数は小数第2位以下に \(933\) という数字の並びが繰り返されています。
無理数を小数で表すと、以下の例のようになります。
\begin{eqnarray}
\pi &=& 3.14159265\cdots \\[0.5em]
\sqrt{5} &=& 2.23606797\cdots
\end{eqnarray}
これらは循環しない無限小数です。
以上の例のように、有理数を小数で表すと有限小数か循環小数に、無理数を小数で表すと循環しない無限小数になります。

循環小数の取り扱い
循環小数には特別な表記法があります。循環する部分の最初と最後の数字の上に”\(\cdot\)”をつける方法です。循環する数字が1つだけなら、その数字の上に”\(\cdot\)”をつけます。
この表記法を用いると、
\begin{eqnarray}
0.333333\cdots &=& 0.\dot{3} \\[.5em]
-2.52525252\cdots &=& -2.\dot{5}\dot{2} \\[.5em]
1.52478654786547865\cdots &=& 1.52\dot{4}786\dot{5} \\[.5em]
\end{eqnarray}
のようになります。
ちなみに、循環小数の循環する部分1つ分を循環節といいます。例えば、
- \(0.\dot{3}\) の循環節は \(3\)
- \(1.52\dot{4}786\dot{5}\) の循環節は \(47865\)
です。
分数を循環小数に変換するのは、割り算をするだけなので簡単ですね。しかし、循環小数から分数への変換はどのように行うのでしょうか?以下の例題でその方法を確認しましょう。
例題
以下の循環小数を分数で表してください。
\((1) \quad 0.\dot{2}4\dot{6}\)
\((2) \quad 1.1\dot{6}\dot{9}\)
解答・解説
\((1)\)
まずは
\[x = 0.\dot{2}4\dot{6} \qquad \cdots(1)\]
とおきます。次に、循環節1つ分が小数点以上にくるように、両辺に同じ数を掛けます。ここでは、両辺を1000倍します。そうすると、
\[1000x = 246.\dot{2}4\dot{6} \qquad \cdots(2)\]
となります。そして、ここからが大事なところです。無限に続く循環節が邪魔なので消してしまいましょう。\((1)\) と \((2)\) を見比べると、小数点以下が同じであることがわかります。よって、\((2)-(1)\) をします。
\begin{align}
\phantom{-\big{)}} 1000x = 246.\dot{2}4\dot{6} \\
\rlap{\underline{\phantom{- \big{)} 1000x = 246.\dot{2}4\dot{6}00}}} – \big{)} \phantom{0000} x = \phantom{00} 0.\dot{2}4\dot{6} \\
999x = 246 \phantom{.000}
\end{align}
あとは簡単な方程式を解くだけです。約分も忘れずにしましょう。
\[x = \frac{246}{999} = \frac{82}{333}\]
よって、答えは
\[0.\dot{2}4\dot{6} = \frac{82}{333}\]
\((2)\)
同じように、まずは
\[y = 1.1\dot{6}\dot{9} \qquad \cdots(3)\]
とおきます。ここで、循環節の最初の数が小数第1位にくるように、\((3)\) の両辺に10を掛けると、
\[10y = 11.\dot{6}\dot{9} \qquad \cdots(4)\]
となります。次に、循環節1つ分が小数点以上にくるように、\((4)\) の両辺に100を掛けると、
\[1000y = 1169.\dot{6}\dot{9} \qquad \cdots(5)\]
となります。ここで、\((5)-(4)\) をすると
\begin{align}
\phantom{-\big{)}} 1000y = 1169.\dot{6}\dot{9} \\
\rlap{\underline{\phantom{- \big{)} 1000y = 1169.\dot{6}\dot{9}00}}} – \big{)} \phantom{00} 10y = \phantom{00} 11.\dot{6}\dot{9} \\
990y = 1158 \phantom{.00}
\end{align}
これを解いて、
\[y = \frac{1158}{990} = \frac{193}{165}\]
よって、答えは
\[1.1\dot{6}\dot{9} = \frac{193}{165}\]
循環小数を分数に変換する手順をまとめておきます。文章だけではわかりにくいので、上の例題と照らし合わせながら確認してください。
- 分数に変換したい循環小数を適当な文字で置く。この式を \((1)\) とする。
- 循環節の最初の数が小数第1位にくるように、\((1)\) 式の両辺に同じ数を掛ける。この式を \((2)\) とする。
- 循環節1つ分が小数点以上にくるように、\((2)\) 式の両辺に同じ数を掛ける。この式を \((3)\) とする。
- \((3)-(2)\) をして、方程式を解き、約分する。
数直線
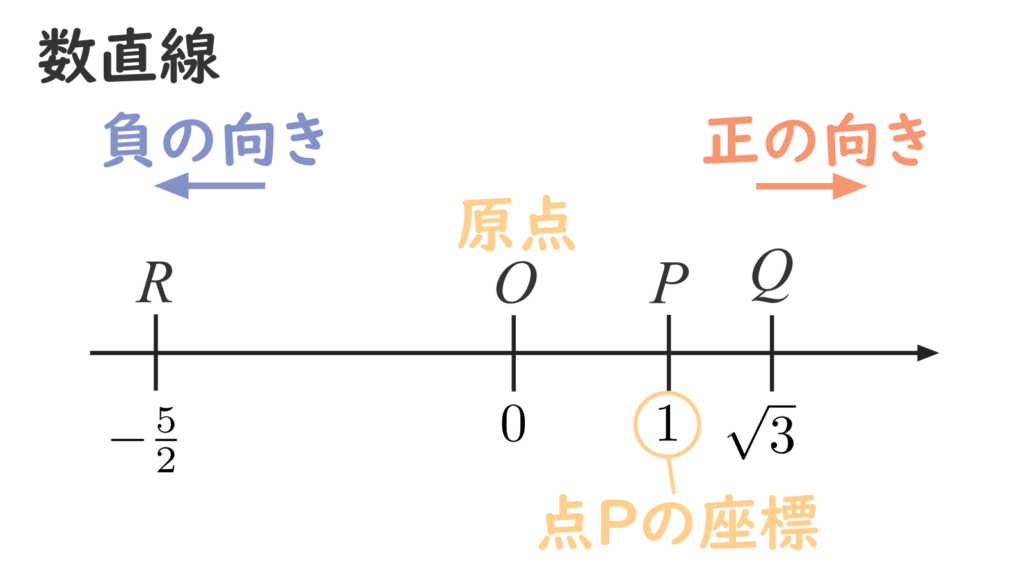
すべての実数は、それぞれ数直線上のただ1つの点として表すことができます。逆に、数直線上のすべての点は、それぞれただ1つの実数を表します。 数直線上の点 \(P\) が実数 \(x\) に対応するとき、\(x\) を点 \(P\) の座標といいます。
数直線上で、実数 \(0\) に対応する点 \(O\) を原点といいます。すなわち、原点 \(O\) の座標は \(0\) です。数直線に描かれた矢印は、数直線の正の向きを表します。一方、その反対の向きは負の向きです。原点より正の向きにある部分には正の実数、負の向きにある部分には負の実数が対応します。
練習問題
問題1
\(\displaystyle \frac{1}{7}\) を小数で表してください。
解答・解説
\(\displaystyle \frac{1}{7}\) を割り算で表すと
\[\frac{1}{7} = 1\div7\]
なので、これを筆算で計算します。
\begin{align}
\phantom{7\big{)}} \rlap{\underline{\phantom{ 0.142857 }}} 0.142857 \\
7 \big{)} \hspace{0.5em} 1.0 \phantom{00000} \\
\rlap{\underline{\phantom{ 70 }}} 7 \phantom{00000} \\
30 \phantom{0000} \\
\rlap{\underline{\phantom{ 280 }}} 28 \phantom{0000} \\
20 \phantom{000} \\
\rlap{\underline{\phantom{ 140 }}} 14 \phantom{000} \\
60 \phantom{00} \\
\rlap{\underline{\phantom{ 560 }}} 56 \phantom{00} \\
40 \phantom{0} \\
\rlap{\underline{\phantom{ 350 }}} 35 \phantom{0} \\
50 \\
\rlap{\underline{\phantom{ 49 }}} 49 \\
1
\end{align}
余り \(1\) が出てきました。これは最初の \(1\) と同じなので、これ以降は同じ計算が繰り返されるはずです。このように、筆算をしているときに同じ余りが出てきたときは、結果が循環小数となります。それ以降を計算する必要はありません。
よって、答えは
\[\frac{1}{7} = 0.142857142857\cdots = 0.\dot{1}4285\dot{7}\]
問題2
以下の小数を分数で表してください。
\((1) \quad 0.00\dot{3}\dot{0}\)
\((2) \quad 0.\dot{9}\)
解答・解説
\((1)\)
解説は省略します。答えは
\[0.00\dot{3}\dot{0} = \frac{1}{330}\]
\((2)\)
\(x=0.\dot{9}\) とおき、手順にそって計算を進めます。そうすると
\begin{align}
\phantom{-\big{)}} 10x = 9.\dot{9} \\
\rlap{\underline{\phantom{- \big{)} 10x = 9.\dot{9}00}}} – \big{)} \phantom{00} x = 0.\dot{9} \\
9x = 9 \phantom{.0} \\
\quad x = 1 \phantom{.0}
\end{align}
となります。よって、答えは
\[0.\dot{9} = 1\]
\(0.999\cdots = 1\) という、直感に反する式を簡単に証明することができました。
今回はこれで終わりです。この記事が気に入っていただけたら、SNS等でのシェアをよろしくお願いします!また、公式Xのフォローやブックマークなどもよろしくお願いします!
質問・感想等はぜひ下のコメント欄に書き込んでください!

