2次式の展開公式
整式の積の形で表された式を、単項式の和の形に表すことを、整式の展開といいます。
展開の基本は分配法則を使うことです。分配法則を使った展開は以下のようになります。
\[2x(x^{2}+3) = 2x^{3} + 6x\]
\[(x-2)(2x+5) = 2x^{2}+5x-4x-10 = 2x^{2}+x-10\]
なお、分配法則については以下の記事で詳しく解説しています。ぜひご覧ください。
ここからは、分配法則を使わなくても簡単に展開できるパターンを紹介します。これらのパターンでは、展開の公式を使うことで展開することができます。以下に2次式の展開公式をまとめたので、しっかりと覚えましょう。
\((\mathrm{i}) \quad (a+b)^{2} = a^{2}+2ab+b^{2}\)
\((\mathrm{ii}) \quad (a-b)^{2} = a^{2}-2ab+b^{2}\)
\((\mathrm{iii}) \quad (a+b)(a-b) = a^{2} – b^{2}\)
\((\mathrm{iv}) \quad (x+a)(x+b) = x^{2}+(a+b)x+ab\)
\((\mathrm{v}) \quad (ax+b)(cx+d) = acx^{2}+(ad+bc)x+bd\)
これらの公式はすべて分配法則から簡単に導くことができます。ここですべての公式を証明してみましょう。
証明
\((\mathrm{i})\)
\((a+b)^{2} = (a+b)(a+b)\) なので、分配法則を使って展開することができます。
\begin{eqnarray}
(a+b)^{2} &=& (a+b)(a+b) \\[.5em]
&=& a^{2}+ab+ba+b^{2} \\[.5em]
&=& a^{2}+2ab+b^{2}
\end{eqnarray}
\((\mathrm{ii})\)
\((\mathrm{i})\) と同じように計算します。
\begin{eqnarray}
(a-b)^{2} &=& (a-b)(a-b) \\[.5em]
&=& a^{2}-ab-ba+b^{2} \\[.5em]
&=& a^{2}-2ab+b^{2}
\end{eqnarray}
\((\mathrm{iii})\)
このまま分配法則を使って展開します。\(ab\) の項はプラスとマイナスで打ち消し合っています。
\begin{eqnarray}
(a+b)(a-b) &=& a^{2}-ab+ba-b^{2} \\[.5em]
&=& a^{2}-b^{2}
\end{eqnarray}
\((\mathrm{iv})\)
こちらもこのまま分配法則を使って展開します。\(ax\) の項と \(bx\) の項は無理やりまとめます。
\begin{eqnarray}
(x+a)(x+b) &=& x^{2}+bx+ax+ab \\[.5em]
&=& x^{2}+(a+b)x+ab
\end{eqnarray}
\((\mathrm{v})\)
これもこのまま分配法則を使って展開します。\(adx\) の項と \(bcx\) の項は無理やりまとめます。
\begin{eqnarray}
(ax+b)(cx+d) &=& ax \cdot cx+ax \cdot d+b \cdot cx+bd \\[.5em]
&=& acx^{2}+adx+bcx+bd \\[.5em]
&=& acx^{2}+(ad+bc)x+bd
\end{eqnarray}
以上ですべての公式を証明することができました。■
わざわざ証明するまでもなかったかもしれませんが、展開公式を忘れてしまっても諦めないでほしいということを証明を通じて伝えたかったのです。たとえ公式を忘れても、分配法則を使えばどんな整式でも必ず展開することができるということを覚えておいてください。
それでは、実際に展開公式を使ってみましょう。
例題1
以下の式を展開してください。
\((1) \quad (x+2)^{2}\)
\((2) \quad (2x-3)^{2}\)
\((3) \quad (x+1)(x-1)\)
\((4) \quad (x+4)(x+5)\)
\((5) \quad (3x+5)(2x-7)\)
解答・解説
\((1)\)
展開公式の \((\mathrm{i}) \ (a+b)^{2} = a^{2}+2ab+b^{2}\) を使います。\(a=x, \ b=2\) として公式に当てはめると、
\begin{eqnarray}
(x+2)^{2} &=& x^{2}+2 \cdot x \cdot 2+2^{2} \\[.5em]
&=& x^{2}+4x+4
\end{eqnarray}
となります。
\((2)\)
展開公式の \((\mathrm{ii}) \ (a-b)^{2} = a^{2}-2ab+b^{2}\) を使います。\(a=2x, \ b=3\) として公式に当てはめると、
\begin{eqnarray}
(2x-3)^{2} &=& (2x)^{2}-2 \cdot 2x \cdot 3+3^{2} \\[.5em]
&=& 4x^{2}-12x+9
\end{eqnarray}
となります。
\((3)\)
展開公式の \((\mathrm{iii}) \ (a+b)(a-b) = a^{2}-b^{2}\) を使います。\(a=x, \ b=1\) として公式に当てはめると、
\begin{eqnarray}
(x+1)(x-1) &=& x^{2} – 1^{2} \\[.5em]
&=& x^{2} – 1
\end{eqnarray}
となります。
\((4)\)
展開公式の \((\mathrm{iv}) \ (x+a)(x+b) = x^{2}+(a+b)x+ab\) を使います。\(a=4, \ b=5\) として公式に当てはめると、
\begin{eqnarray}
(x+4)(x+5) &=& x^{2}+(4+5)x+4\cdot 5 \\[.5em]
&=& x^{2}+9x+20
\end{eqnarray}
となります。
公式 \((\mathrm{iv})\) は、1次の項の係数は足し算、定数項は掛け算と覚えましょう。分配法則を思い出せば、逆に計算してしまうことはないはずです。
\((5)\)
展開公式の \((\mathrm{v}) \ (ax+b)(cx+d) = acx^{2}+(ad+bc)x+bd\) を使います。\(a=3, \ b=5, \ c=2, \ d=-7\) として公式に当てはめると、
\begin{eqnarray}
(3x+5)(2x-7) &=& 3\cdot 2x^{2}+(3\cdot (-7)+5 \cdot 2)x+5 \cdot (-7) \\[.5em]
&=& 6x^{2}+(-21+10)x-35 \\[.5em]
&=& 6x^{2}-11x-35
\end{eqnarray}
となります。
公式 \((\mathrm{v})\) は少し覚えにくいですが、2次の項は左側の項の掛け算、1次の項の係数は(外×外)+(内×内)、定数項は右側の項の掛け算です。言葉ではわかりにくいので、下の画像も参考にしてください。
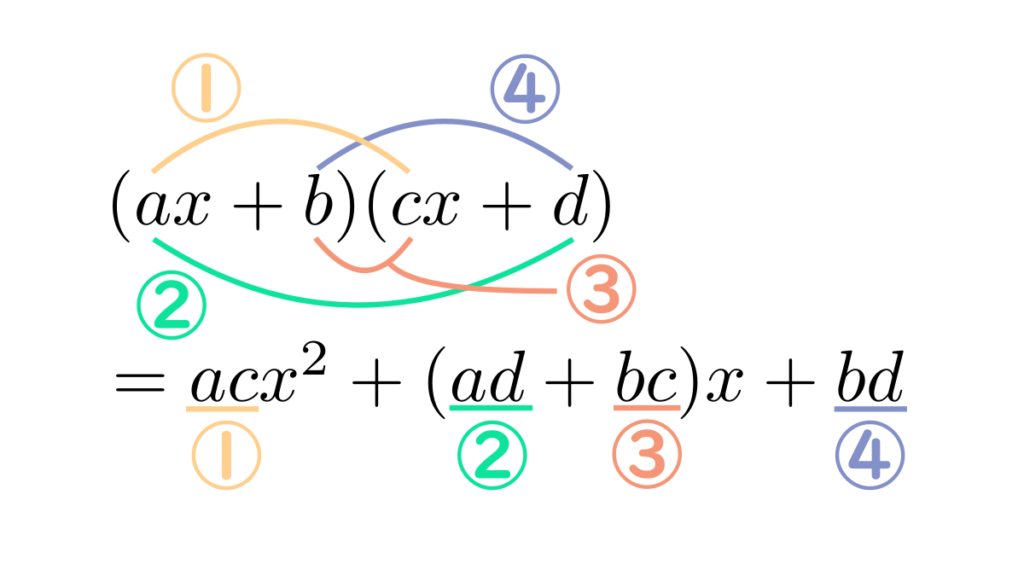
3次式の展開公式
ここからは3次式の展開公式を紹介します。
\((\mathrm{vi}) \quad (a+b)^{3} = a^{3}+3a^{2}b+3ab^{2}+b^{3}\)
\((\mathrm{vii}) \quad (a-b)^{3} = a^{3}-3a^{2}b+3ab^{2}-b^{3}\)
\((\mathrm{viii}) \quad (a+b)(a^{2}-ab+b^{2}) = a^{3}+b^{3}\)
\((\mathrm{ix}) \quad (a-b)(a^{2}+ab+b^{2}) = a^{3}-b^{3}\)
これらの公式もすべて分配法則から導くことができます。ここでは \((\mathrm{vi})\) と \((\mathrm{viii})\) の公式を証明してみます。
証明
\((\mathrm{vi})\)
\((a+b)^{3} = (a+b)^{2}(a+b)\) なので、まずは \((a+b)^{2}\) を公式 \((\mathrm{i})\) を使って展開します。
\begin{eqnarray}
(a+b)^{3} &=& (a+b)^{2}(a+b) \\[.5em]
&=& (a^{2}+2ab+b^{2})(a+b)
\end{eqnarray}
あとは分配法則を使って展開すると、
\begin{align}
&(a^{2}+2ab+b^{2})(a+b) \\[.5em]
&= a^{2} \cdot a + a^{2} \cdot b + 2ab \cdot a + 2ab \cdot b + b^{2} \cdot a + b^{2} \cdot b \\[.5em]
&= a^{3} + a^{2}b + 2a^{2}b + 2ab^{2} + ab^{2} + b^{3} \\[.5em]
&= a^{3}+3a^{2}b+3ab^{2}+b^{3}
\end{align}
となります。
\((\mathrm{viii})\)
このまま分配法則を使って展開します。\(a^{2}b\) の項と \(ab^{2}\) の項はプラスとマイナスで打ち消し合っています。
\begin{align}
&(a+b)(a^{2}-ab+b^{2}) \\[.5em]
&= a \cdot a^{2} + a \cdot (-ab) + a \cdot b^{2} + b \cdot a^{2} + b \cdot (-ab) + b \cdot b^{2} \\[.5em]
&= a^{3} – a^{2}b + ab^{2} + a^{2}b – ab^{2} + b^{3} \\[.5em]
&= a^{3}+b^{3}
\end{align}
以上で \((\mathrm{vi})\) と \((\mathrm{viii})\) の公式を証明することができました。■
\((\mathrm{vii})\) と \((\mathrm{ix})\) の公式も同様に証明できるので、ぜひやってみてください。3次式の展開公式はとっつきにくいイメージがあるかもしれませんが、証明を通じて2次式の展開公式との類似点を理解していただけたら幸いです。
それでは、例題で3次式の展開公式を使ってみましょう。
例題2
以下の式を展開してください。
\((1) \quad (3x+2)^{3}\)
\((2) \quad (x-5)^{3}\)
\((3) \quad (x+1)(x^{2}-x+1)\)
\((3) \quad (2x-5)(4x^{2}+10x+25)\)
解答・解説
\((1)\)
展開公式の \((\mathrm{vi}) \ (a+b)^{3} = a^{3}+3a^{2}b+3ab^{2}+b^{3}\) を使います。\(a=3x, \ b=2\) として公式に当てはめると、
\begin{eqnarray}
(3x+2)^{3} &=& (3x)^{3}+3 \cdot (3x)^{2} \cdot 2+3 \cdot 3x \cdot 2^{2}+2^{3} \\[.5em]
&=& 27x^{3}+54x^{2}+36x+8
\end{eqnarray}
となります。
\((2)\)
展開公式の \((\mathrm{vii}) \ (a-b)^{3} = a^{3}-3a^{2}b+3ab^{2}-b^{3}\) を使います。\(a=x, \ b=5\) として公式に当てはめると、
\begin{eqnarray}
(x-5)^{3} &=& x^{3}-3 \cdot x^{2} \cdot 5+3 \cdot x \cdot 5^{2}-5^{3} \\[.5em]
&=& x^{3}-15x^{2}+75x-125
\end{eqnarray}
となります。
公式 \((\mathrm{vii})\) はプラスとマイナスが交互に現れることに注意しましょう。
\((3)\)
展開公式の \((\mathrm{viii}) \ (a+b)(a^{2}-ab+b^{2}) = a^{3}+b^{3}\) を使います。\(a=x, \ b=1\) とすると、\(a^{2}-ab+b^{2} = x^{2}-x+1\) となっているので、公式が使えることが分かります。
\[(x+1)(x^{2}-x+1) = x^{3}+1^{3} = x^{3}+1\]
\((4)\)
展開公式の \((\mathrm{ix}) \ (a-b)(a^{2}+ab+b^{2}) = a^{3}-b^{3}\) を使います。\(a=2x, \ b=5\) とすると、\(a^{2}+ab+b^{2} = 4x^{2}+10x+25\) となっているので、公式が使えることが分かります。
\[(2x-5)(4x^{2}+10x+25) = (2x)^{3}-5^{3} = 8x^{3}-125\]
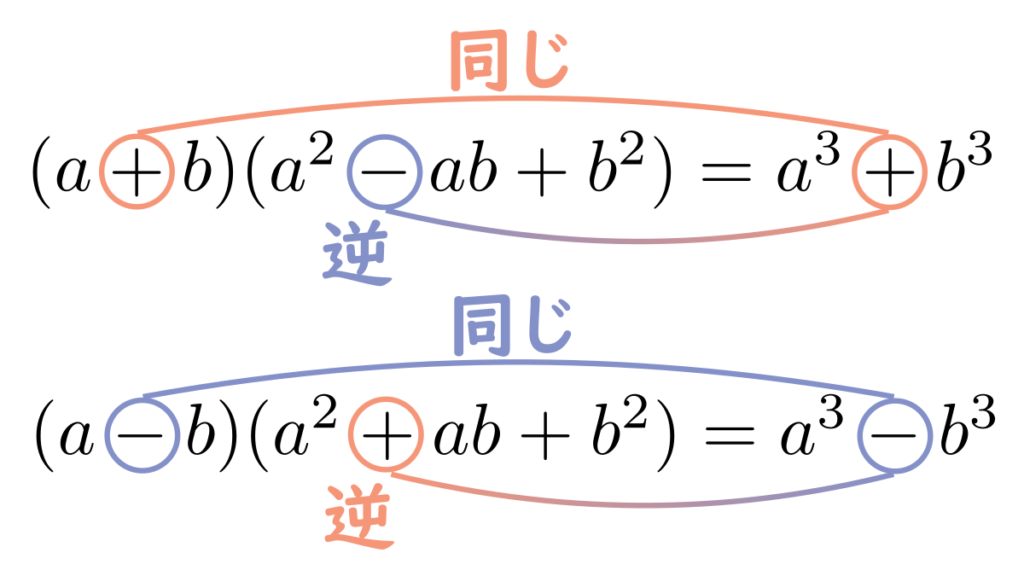
公式 \((\mathrm{viii})\) と公式 \((\mathrm{ix})\) は符号に注意が必要です。以下の画像もぜひ参考にしてください。
練習問題
問題
以下の式を展開してください。
\((1) \quad (x-4)(x-3)\)
\((2) \quad (a+2b)^{2}\)
\((3) \quad (3x+4)(x+2)\)
\(\displaystyle (4) \quad \left( x+\frac{1}{3} \right) \left(x-\frac{1}{3} \right) \)
\((5) \quad (9a^{2}+b^{2}+3ab)(3a-b)\)
\((6) \quad (2x-3y)^{3}\)
解答・解説
\((1)\)
展開公式の \((\mathrm{iv}) \ (x+a)(x+b) = x^{2}+(a+b)x+ab\) を使います。
\begin{eqnarray}
(x-4)(x-3) &=& x^{2}+(-4-3)x+(-4)\cdot (-3) \\[.5em]
&=& x^{2}-7x+12
\end{eqnarray}
\((2)\)
展開公式の \((\mathrm{i}) \ (a+b)^{2} = a^{2}+2ab+b^{2}\) を使います。
\begin{eqnarray}
(a+2b)^{2} &=& a^{2}+2 \cdot a \cdot 2b+(2b)^{2} \\[.5em]
&=& a^{2}+4ab+4b^{2}
\end{eqnarray}
\((3)\)
展開公式の \((\mathrm{v}) \ (ax+b)(cx+d) = acx^{2}+(ad+bc)x+bd\) を使います。ここでは、\(c=1\) と考えて公式を使います。
\begin{eqnarray}
(3x+4)(x+2) &=& 3 \cdot 1x^{2} + (3 \cdot 2 + 4 \cdot 1)x +4 \cdot 2 \\[.5em]
&=& 3x^{2}+10x+8
\end{eqnarray}
\((4)\)
展開公式の \((\mathrm{iii}) \ (a+b)(a-b) = a^{2}-b^{2}\) を使います。分数が入っていても気にする必要はありません。
\begin{eqnarray}
\left( x+\frac{1}{3} \right) \left(x-\frac{1}{3} \right) &=& x^{2}-\left( \frac{1}{3}\right) ^{2} \\[.5em]
&=& x^{2}-\frac{1}{9}
\end{eqnarray}
\((5)\)
このままだと分かりにくいので、少し式を並び替えてみます。
\[(9a^{2}+b^{2}+3ab)(3a-b) = (3a-b)(9a^{2}+3ab+b^{2})\]
これで展開公式の \((\mathrm{ix}) \ (a-b)(a^{2}+ab+b^{2}) = a^{3}-b^{3}\) が使えるということが分かりやすくなりました。実際、\(a=3a, \ b=b\) とすると、\(a^{2}+ab+b^{2} = 9a^{2}+3ab+b^{2}\) となっているので、公式 \((\mathrm{ix})\) が使えることがわかります。
\[(3a-b)(9a^{2}+3ab+b^{2}) = (3a)^{3}-b^{3} = 9a^{3}-b^{3}\]
\((6)\)
展開公式の \((\mathrm{vii}) \ (a-b)^{3} = a^{3}-3a^{2}b+3ab^{2}-b^{3}\) を使います。
\begin{eqnarray}
(2x-3y)^{3} &=& (2x)^{3}-3 \cdot (2x)^{2} \cdot 3y+3 \cdot 2x \cdot (3y)^{2}-(3y)^{3} \\[.5em]
&=& 8x^{3}-36x^{2}y+54xy^{2}-27y^{3}
\end{eqnarray}
今回はこれで終わりです。この記事が気に入っていただけたら、SNS等でのシェアをよろしくお願いします!また、公式Xのフォローやブックマークなどもよろしくお願いします!

